Rezolvarea integralelor. Vă spunem cum să rezolvați integralele.

Integrală este un concept matematic extins de sumă. Rezolvarea integralelor sau găsirea lor se numește integrare. Folosind integrala, puteți găsi cantități precum suprafața, volumul, masa și multe altele. Rezolvarea integralelor(integrarea) este operația inversă de diferențiere. Pentru a înțelege mai bine ce este o integrală, să o prezentăm în forma următoare. Imagina. Avem un corp, dar nu îl putem descrie încă, știm doar ce particule elementare are și cum sunt localizate. Pentru a asambla un corp într-un singur întreg, este necesar să se integreze particulele sale elementare - să fuzioneze părțile într-un singur sistem. În formă geometrică pentru funcția y=f(x), integrala reprezintă aria figurii delimitată de curbă, axa x și 2 linii verticale x=a și x=b.

Deci, aria zonei umbrite este integrala funcției în intervalul de la a la b. Nu crezi? Să verificăm orice funcție. Să luăm cea mai simplă y=3. Să limităm funcția la valorile a=1 și b=2. Să construim: Deci cifra limitată este un dreptunghi. Aria unui dreptunghi este egală cu produsul dintre lungime și lățime. În cazul nostru, lungime 3, lățime 1, suprafață 3*1=3. Să încercăm să rezolvăm același lucru fără a recurge la construcție, folosind integrare: După cum puteți vedea, răspunsul a fost același. Rezolvarea integralelor înseamnă colectarea unor părți elementare într-una singură. În cazul suprafeței, se însumează benzi de lățime infinitezimală. Integralele pot fi definite sau nedefinite. Rezolvarea unei integrale definite înseamnă găsirea valorii unei funcții în limite date. Rezolvarea integralei nedefinite se rezumă la găsirea antiderivatei. F(x) este o antiderivată. Diferențiând antiderivatul, obținem expresia integrandului original. Pentru a verifica dacă am rezolvat corect integrala, diferențiem răspunsul rezultat și îl comparăm cu expresia originală. Principalele funcții și antiderivate ale acestora sunt prezentate în tabel:

Tabel cu antiderivate pentru rezolvarea integralelor

Tehnici de bază pentru rezolvarea integralelor: Rezolvarea unei integrale înseamnă integrarea unei funcții peste o variabilă. Dacă integrala are o formă tabelară, atunci putem spune că a fost rezolvată problema cum se rezolvă integrala. Dacă nu, atunci sarcina principală atunci când rezolvați integrala este reducerea acesteia la formă tabelară. Mai întâi trebuie să vă amintiți proprietățile de bază ale integralelor:

Cunoașterea doar a acestor elemente de bază vă va permite să rezolvați integrale simple. Dar trebuie înțeles că majoritatea integralelor sunt complexe și pentru a le rezolva este necesar să se recurgă la utilizarea unor tehnici suplimentare. Mai jos ne vom uita la principalele exemple de rezolvare a integralelor. Recepțiile vor fi oferite pentru informații generale. nici un exemplu de soluții pentru a nu supraîncărca articolul. Trebuie să înțelegeți că în 5 minute de citire a articolului nu veți învăța să rezolvați toate integralele complexe, dar un cadru corect format de înțelegere va economisi ore de timp pe învățarea și dezvoltarea abilităților de rezolvare a integralelor.

Tehnici de bază pentru rezolvarea integralelor

1. Înlocuire variabilă.
Pentru a efectua această tehnică, veți avea nevoie de o bună abilitate în găsirea derivatelor.

2. IntegrareÎn părți. Utilizați următoarea formulă. Aplicarea acestei formule permite ca integralele aparent de nerezolvat să fie aduse la o soluție.

3. Integrare funcții raționale fracționale. - descompune o fracție în forma sa cea mai simplă - selectați un pătrat complet - creați o diferență a numitorului în numărător.

4. Integrare funcții iraționale fracționale. - selectați un pătrat complet sub rădăcină - se creează o diferenţială de expresie radicală în numărător. 5. Integrarea funcţiilor trigonometrice. La integrarea expresiilor formei, aplică formule de expansiune pentru produs. Pentru expresii m-impar, n-orice, creați d(cosx). Folosim identitatea sin 2 +cos 2 =1 m,n – par, sin 2 x=(1-cos2x)/2 și cos 2 x=(1+cos2x)/2 Pentru expresii de forma: - Se aplică proprietatea tg 2 x=1/cos 2 x – 1

1. Înțelegeți esența integralelor. Este necesar să înțelegem esența de bază a integralei și soluțiile sale. O integrală este în esență suma părților elementare ale obiectului integrării. Dacă vorbim despre integrarea unei funcții, atunci integrala este aria figurii dintre graficul funcției, axa x și limitele integrării. Dacă integrala este nedefinită, adică limitele integrării nu sunt indicate, atunci soluția se rezumă la găsirea unei antiderivate. Dacă integrala este definită, atunci este necesar să înlocuiți valorile limitelor în funcția găsită. 2. Exersați utilizarea tabelului de antiderivate și proprietățile de bază ale integralelor. Trebuie să învățați cum să utilizați tabelul antiderivate. Pentru o varietate de funcții, antiderivatele sunt găsite și introduse în tabel. Dacă avem o integrală care se află în tabel, putem spune că a fost rezolvată. 3. Înțelegerea tehnicilor și dezvoltarea abilităților de rezolvare a integralelor. Dacă integrala nu este de formă tabelară, atunci soluția ei se reduce la reducerea ei la forma uneia dintre integralele tabulare. Pentru a face acest lucru, folosim proprietățile de bază și tehnicile de soluție. Dacă în unele etape ale aplicării tehnicilor întâmpinați dificultăți și neînțelegeri, atunci înțelegeți mai detaliat această tehnică specială, priviți exemplele unui plan similar și întrebați profesorul. În plus după rezolvarea integralei Se recomandă verificarea soluției în primele etape. Pentru a face acest lucru, diferențiem expresia rezultată și o comparăm cu integrala originală. Să rezolvăm punctele principale folosind mai multe exemple:

Exemple de rezolvare a integralelor

Exemplul 1: Rezolvați integrala: Integrala este nedefinită. Găsim antiderivatul. Pentru a face acest lucru, descompunem integrala sumei în suma integralelor. Fiecare dintre integrale este sub formă tabelară. Să ne uităm la antiderivatele din tabel. Rezolvarea integralei: Să verificăm soluția (găsește derivata).

Pentru rezolvarea exercițiilor pe tema „Integrare”, se recomandă următoarea literatură:

1. . Analiza matematică. Integrală nedefinită. Integrală definită: tutorial. – M.: MGIU, 2006. – 114 p.: ill. 20.

2., etc. Probleme și exerciții de analiză matematică pentru colegii/Ed. . (orice an de publicare).

Seminarul nr. 1.

Găsirea integralelor nedefinite folosind regulile de bază de integrare și un tabel de integrale nedefinite.

https://pandia.ru/text/78/291/images/image002_164.gif" width="113 height=27" height="27">, apoi,

unde C este o constantă arbitrară,

2) unde k– valoare constantă,

4) .

https://pandia.ru/text/78/291/images/image008_45.gif" width="24" height="28 src="> Sub semnul integral se află produsul a două constante, care este, desigur, de asemenea o constantă Conform regulii de bază a integrării 2), o luăm în afara semnului integral.

(2) Folosim formula 1) Tabele de integrale.

https://pandia.ru/text/78/291/images/image010_36.gif" width="569" height="44 src=">.gif" width="481" height="75 src=">

https://pandia.ru/text/78/291/images/image014_25.gif" width="255" height="32 src=">. În cazul nostru, https://pandia.ru/text/78/ 291/images/image017_22.gif" width="75 height=47" height="47">, apoi .

(3) Să folosim regula de bază 3) a integrării (integrala sumei funcțiilor este egală cu suma integralelor acestor funcții).

(4) Folosim formula 1) Tabelul integralelor și regula de bază a integrării 4), punând , i.e.

.

https://pandia.ru/text/78/291/images/image022_9.gif" width="551" height="91 src=">

https://pandia.ru/text/78/291/images/image024_8.gif" width="449" height="101 src=">.

(1) Să folosim formula de înmulțire prescurtată

https://pandia.ru/text/78/291/images/image026_7.gif" width="103" height="37 src=">).

(2) Folosim proprietatea puterilor ( ).

(4) În fiecare dintre termenii de sub semnul integral folosim proprietatea puterilor (https://pandia.ru/text/78/291/images/image029_7.gif" width="325" height="56 src= „>.

(1) Să schimbăm doi termeni în numitorul integrandului pentru a obține o integrală tabelară.

(2) Să folosim formula 6) Tabele de integrale..gif" width="364 height=61" height="61">.

(1) Să schimbăm cei doi termeni sub semnul rădăcinii în numitorul integrandului pentru a obține o integrală de tabel.

(2) Să folosim formula 11) Tabele de integrale.

https://pandia.ru/text/78/291/images/image033_5.gif" width="625" height="75 src=">

https://pandia.ru/text/78/291/images/image035_5.gif" width="459" height="67 src=">

https://pandia.ru/text/78/291/images/image037_5.gif" width="535" height="67 src=">

(1) Înlocuitor .

(2) Din identitatea trigonometrică de bază avem .

(3) Împărțiți fiecare termen al termenului numărător cu termen la numitor.

(4) Să folosim regula de bază 3) a integrării (integrala sumei funcțiilor este egală cu suma integralelor acestor funcții).

(5) Folosim formula 15) din Tabelul Integralelor și regula de bază a integrării 4), punând , i.e. .

Exerciții. Nr. 000, 1034, 1036, 1038, 1040, 1042, 1044, 1046, 1048 (a) din cartea de probleme.

Seminarul nr. 2

Integrarea prin schimbarea metodei variabilei

Dacă integrala nu este tabelară, atunci este adesea folosită o înlocuire variabilă, și anume, presupunând https://pandia.ru/text/78/291/images/image044_5.gif" width="39" height="27 src=" > - functie continuu diferentiabila.Inlocuind in integrala avem

Obținem funcția https://pandia.ru/text/78/291/images/image043_5.gif" width="71" height="27"> și o substituim în antiderivată, în funcție de variabilă t, rezultând o antiderivată în funcție de variabila inițială X, adică revenim la vechea variabilă. Cu siguranță ar trebui să reveniți la vechea variabilă!

În acest exemplu, înlocuirea variabilei este deja specificată.

https://pandia.ru/text/78/291/images/image049_5.gif" width="525" height="115 src=">

https://pandia.ru/text/78/291/images/image051_3.gif" width="408" height="83 src=">

https://pandia.ru/text/78/291/images/image053_3.gif" width="256 height=67" height="67">, din .

La înlocuire avem .

(2) Înmulțiți numărătorul și numitorul cu .

(3) Această integrală este „asemănătoare” cu tabelele 9) și 10), dar rețineți că în ambele coeficientul pentru pătratul necunoscutului este egal cu 1. Prin urmare, sub rădăcină, luăm coeficientul pentru din paranteze.

(4) Folosim proprietatea rădăcinii pătrate a produsului a doi factori pozitivi: dacă și , atunci .

(5) Selectăm un factor sub semnul integral.

(6) Scoatem acest factor din semnul integral, conform Regulii de bază 2) a integrării.

(7) Conform formulei 10) Tabelul integralelor nedefinite, obținem un răspuns în funcție de variabila . Aici , .

(8) Ne întoarcem la vechea variabilă, făcând o înlocuire inversă, adică gif" width="611" height="115 src="> =

https://pandia.ru/text/78/291/images/image067_2.gif" width="47" height="21"> avem , de exemplu.

(2) Folosim identitatea logaritmică de bază: https://pandia.ru/text/78/291/images/image071_2.gif" width="111 height=32" height="32">.

(3) Aducem expresia din numitor la un numitor comun.

(4) Înmulțiți numărătorul și numitorul integrandului cu https://pandia.ru/text/78/291/images/image072_2.gif" width="581" height="53 src=">

https://pandia.ru/text/78/291/images/image074_2.gif" width="179" height="53 src=">. Să ne amintim asta pentru viitor.

În acest exemplu, este deja specificată înlocuirea variabilei.

https://pandia.ru/text/78/291/images/image076_2.gif" width="621" height="64 src=">.

Foarte des este recomandabil să încercați o înlocuire dacă expresia se află sub semnul integral sau o înlocuire https://pandia.ru/text/78/291/images/image080_2.gif" width="80" height="33" >unde - un număr întreg pozitiv Diferenţial" href="/text/category/differentcial/" rel="bookmark">diferenţial .

Dacă integrandul depinde de expresia , atunci pot fi date câteva recomandări pentru schimbarea variabilei.

https://pandia.ru/text/78/291/images/image085.jpg" width="600" height="372 src=">

https://pandia.ru/text/78/291/images/image087_2.gif" width="557" height="68 src=">

https://pandia.ru/text/78/291/images/image089_2.gif" width="343" height="64 src=">

https://pandia.ru/text/78/291/images/image091_2.gif" width="591" height="101 src=">

https://pandia.ru/text/78/291/images/image093_2.gif" width="597" height="101 src=">

https://pandia.ru/text/78/291/images/image095_2.gif" width="113" height="27">..gif" width="108" height="27 src=">.

Într-adevăr,

https://pandia.ru/text/78/291/images/image099_2.gif" width="125" height="27 src=">

Adică, în cazul în care funcția integrand are forma https://pandia.ru/text/78/291/images/image100_2.gif" width="48" height="27"> sub semnul diferențial:

https://pandia.ru/text/78/291/images/image102_2.gif" width="292" height="29 src=">. În continuare, înlocuim variabila.

Acest tip de transformare este uneori numit „subsumare sub semnul diferențial”.

Înainte de a analiza exemple pe această temă, vă prezentăm un tabel care poate fi obținut din tabelul integralelor nedefinite

https://pandia.ru/text/78/291/images/image105_1.gif" width="96" height="53 src=">.gif" width="135" height="53 src=">,

https://pandia.ru/text/78/291/images/image109_1.gif" width="147" height="55 src=">,

https://pandia.ru/text/78/291/images/image111_1.gif" width="172" height="60 src=">,

https://pandia.ru/text/78/291/images/image113_1.gif" width="155" height="23 src=">,

https://pandia.ru/text/78/291/images/image115_1.gif" width="128" height="55 src=">,

https://pandia.ru/text/78/291/images/image117_1.gif" width="209" height="53 src=">,

https://pandia.ru/text/78/291/images/image119_1.gif" width="215" height="53 src="> etc.

https://pandia.ru/text/78/291/images/image121_1.gif" width="393" height="48 src=">.

https://pandia.ru/text/78/291/images/image123_1.gif" width="587" height="101 src=">

https://pandia.ru/text/78/291/images/image125_1.gif" width="155" height="27">, atunci se recomandă înlocuirea . Atunci noi avem

https://pandia.ru/text/78/291/images/image128_1.gif" width="592" height="88 src=">=

.

https://pandia.ru/text/78/291/images/image133_1.gif" width="560" height="60 src=">

.

https://pandia.ru/text/78/291/images/image136_1.gif" width="560" height="59 src=">.

Exercițiile nr. 000, 1088, 1151, 1081, 1082, 1094.

Seminarul nr. 4

Metoda de integrare pe părți într-o integrală nedefinită

Această metodă se bazează pe următoarea teoremă.

Teorema. Fie ca funcțiile să aibă derivate finite în interval, iar în acest interval există o antiderivată pentru funcție. Atunci în interval există o antiderivată pentru funcție și formula este valabilă

Această formulă poate fi scrisă ca

.

Sarcina la integrarea pe părți este de a reprezenta integrandul ca produs, astfel încât integrala să fie mai simplă decât , adică nu poate fi aleasă în mod arbitrar, deoarece se poate obține o integrală mai complexă https://pandia.ru/text /78/ 291/images/image149_1.gif" width="45 height=29" height="29">.

Practica arată că majoritatea integralelor „luate” în părți pot fi împărțite în trei grupuri:

https://pandia.ru/text/78/291/images/image151.jpg" width="636" height="396 src=">

Aceste integrale se găsesc prin integrare dublă pe părți.

cometariu. În primul grup de integrale pentru integrale în schimb, poate exista un polinom în funcție de un grad întreg opțional pozitiv (de exemplu https://pandia.ru/text/78/291/images/image156_0.gif" width="33" height="28 src=">. gif" width= "35" height="45 src="> etc.).

În acest exemplu, factorizarea este singura posibilă, ceea ce nu se întâmplă foarte des.

La găsirea expresiei pentru în metoda integrării pe părți, constanta C poate fi setat egal cu zero (vezi p. 22).

https://pandia.ru/text/78/291/images/image163_0.gif" width="552" height="57 src=">

https://pandia.ru/text/78/291/images/image165_0.gif" width="623" height="176 src=">

https://pandia.ru/text/78/291/images/image167_0.gif" width="512" height="53 src=">

https://pandia.ru/text/78/291/images/image169_0.gif" width="25" height="23"> poate fi reprezentat ca ..gif" width="93" height="53 src= " >.

https://pandia.ru/text/78/291/images/image174_0.gif" width="503" height="33 src=">.

Acesta este, de asemenea, un exemplu din al doilea grup de integrale.

https://pandia.ru/text/78/291/images/image176_0.gif" width="591" height="72 src=">

https://pandia.ru/text/78/291/images/image178_0.gif" width="197" height="28 src=">.

Astfel, obținem o ecuație pentru integrala dorită https://pandia.ru/text/78/291/images/image180_0.gif" width="212 height=28" height="28">.

Mutăm termenul în partea stângă a ecuației și obținem ecuația echivalentă

Rezolvând care, obținem răspunsul:

.

Acest exemplu este din al treilea grup de integrale. Aici am folosit integrarea pe părți de două ori.

Exerciții. №№ 000, 1214, 1226, 1221, 1217, 1218, 1225, 1223,

Seminarul nr. 5

Calculul integralelor definite

Calculul integralelor definite se bazează pe proprietățile integralei definite și pe formula Newton-Leibniz.

Să prezentăm principalele proprietăți ale integralei definite

1) Oricare ar fi numerele A, b, cîntotdeauna există egalitate

https://pandia.ru/text/78/291/images/image185_0.gif" width="188" height="61 src=">.

3) Integrala definită a sumei algebrice a două funcții (număr finit) este egală cu suma algebrică a integralelor lor, i.e.

https://pandia.ru/text/78/291/images/image187_0.gif" width="47" height="27 src="> există o antiderivată a unei funcții continue, atunci formula este valabilă

.

Calcularea integralei definite ca limită a sumelor integrale este o sarcină destul de intensivă în muncă, chiar și pentru funcțiile elementare. Formula Newton-Leibniz vă permite să reduceți calculul unei integrale definite la găsirea integralei nedefinite atunci când este cunoscută antiderivată a integrandului. Valoarea integralei definite este egală cu diferența dintre valorile antiderivatei la limitele superioare și inferioare de integrare.

Exemple de calcul a unei integrale definite în cele mai simple cazuri

https://pandia.ru/text/78/291/images/image191_0.gif" width="28" height="71 src=">.gif" width="387" height="61 src=">. gif" width="40" height="28 src=">.gif" width="41" height="21 src=">.gif" width="541" height="67 src=">

https://pandia.ru/text/78/291/images/image199.jpg" width="600" height="145 src=">

.

Atunci când se folosește metoda de modificare a unei variabile într-o integrală definită, trebuie să se țină cont de două puncte.

https://pandia.ru/text/78/291/images/image202.jpg" width="648" height="60 src=">

https://pandia.ru/text/78/291/images/image204.gif" width="319" height="61 src=">.gif" width="89" height="32 src=">. gif" width="525" height="28 src=">.

Integrarea pe părți într-o integrală definită

Când utilizați formula pentru integrarea prin părți într-o integrală definită, uneori se dovedește, de exemplu, că , așa că ar trebui să calculați imediat expresia fără a întârzia până când este găsită întreaga antiderivată.

https://pandia.ru/text/78/291/images/image213.gif" width="29" height="91 src=">.gif" width="221" height="53 src=">. gif" width="365" height="59 src=">.

Exerciții. №№ 000, 1522, 1525, 1531, 1583, 1600,1602.

Seminarul nr. 6

Integrale improprii

Integrale improprii de primul fel

Integralele improprie de primul fel sunt integrale cu limite infinite (sau o limită infinită). Acestea sunt integrale de forma , , . Fie ca funcția să fie integrabilă pe orice segment finit conținut în intervalul de integrare. Apoi, prin definiție

https://pandia.ru/text/78/291/images/image222.gif" width="227 height=60" height="60">.gif" width="235 height=76" height="76" >.

Dacă limitele date există și sunt finite, atunci se spune că integralele improprie converg. Dacă nu există sau sunt infinite, atunci ei spun că ele diverge (pentru mai multe detalii, vezi pp. 72-76).

https://pandia.ru/text/78/291/images/image226.gif" width="47" height="21 src="> avem

https://pandia.ru/text/78/291/images/image228.gif" width="31" height="71 src=">.gif" width="191" height="88 src=">

Dacă https://pandia.ru/text/78/291/images/image232.gif" width="188" height="60 src=">.gif" width="199" height="43 src="> .

Astfel, această integrală converge la și diverge la.

Examinați integrala improprie pentru convergență

https://pandia.ru/text/78/291/images/image239.gif" width="31" height="71 src=">=

https://pandia.ru/text/78/291/images/image241.gif" width="417" height="56 src=">,

Examinați integrala improprie pentru convergență

.

https://pandia.ru/text/78/291/images/image244.gif" width="303" height="61">.gif" width="523" height="59 src=">,

adică această integrală improprie converge.

Găsirea unei integrale nedefinite (un set de antiderivate sau „antiderivate”) înseamnă reconstruirea unei funcții din derivata cunoscută a acestei funcții. Set restaurat de antiderivate F(X) + CU pentru functie f(X) ia în considerare constanta de integrare C. Pe baza vitezei de mișcare a unui punct material (derivată), legea de mișcare a acestui punct (antiderivată) poate fi restabilită; în funcție de accelerația mișcării unui punct – viteza acestuia și legea mișcării. După cum puteți vedea, integrarea este un domeniu larg pentru activitățile fizicii lui Sherlock Holmes. Și în economie, multe concepte sunt reprezentate prin funcții și derivatele lor și, prin urmare, de exemplu, este posibil să se restabilească volumul de produse produse la momentul corespunzător folosind productivitatea muncii la un anumit moment în timp (derivat).

Găsirea unei integrale nedefinite necesită un număr destul de mic de formule de integrare de bază. Dar procesul de găsire a acestuia este mult mai dificil decât doar aplicarea acestor formule. Toată complexitatea nu ține de integrare, ci de aducerea expresiei integrabile într-o formă care să facă posibilă găsirea integralei nedefinite folosind formulele de bază menționate mai sus. Aceasta înseamnă că pentru a începe să exersezi integrarea, trebuie să activezi abilitățile de transformare a expresiei pe care le-ai dobândit în liceu.

Vom învăța să găsim integrale folosind proprietăți și tabel de integrale nedefinite dintr-o lecție despre conceptele de bază ale acestui subiect (se deschide într-o fereastră nouă).

Există mai multe metode de găsire a integralei, dintre care metoda de înlocuire a variabileiȘi metoda integrarii prin piese- un set de domn obligatoriu pentru toți cei care au promovat cu succes matematica superioară. Cu toate acestea, este mai util și mai plăcut să începeți stăpânirea integrării folosind metoda expansiunii, bazată pe următoarele două teoreme privind proprietățile integralei nedefinite, pe care le repetăm ​​aici pentru comoditate.

Teorema 3. Factorul constant din integrand poate fi scos din semnul integralei nedefinite, i.e.

Teorema 4. Integrala nedefinită a unei sume algebrice a unui număr finit de funcții este egală cu suma algebrică a integralelor nedefinite ale acestor funcții, i.e.

(2)

În plus, următoarea regulă poate fi utilă în integrare: dacă expresia integrandului conține un factor constant, atunci expresia antiderivatei este înmulțită cu inversul factorului constant, adică

(3)

Deoarece aceasta este o lecție introductivă în rezolvarea problemelor de integrare, este important să rețineți două lucruri care, fie la început, fie puțin mai târziu, vă pot surprinde. Surpriza se datorează faptului că integrarea este operația inversă a diferențierii și integrala nedefinită poate fi numită pe bună dreptate „antiderivată”.

Primul lucru de care nu ar trebui să fii surprins atunci când integrezi.În tabelul integralelor există formule care nu au analogi între formulele de tabel derivat . Acestea sunt următoarele formule:

Cu toate acestea, vă puteți asigura că derivatele expresiilor din partea dreaptă a acestor formule coincid cu integranții corespunzători.

Al doilea lucru care nu ar trebui să fie surprinzător la integrare. Deși derivata oricărei funcții elementare este și o funcție elementară, integralele nedefinite ale unor funcții elementare nu mai sunt funcții elementare . Exemple de astfel de integrale ar putea fi următoarele:

Pentru dezvoltarea tehnicilor de integrare vor fi utile următoarele abilități: reducerea fracțiilor, împărțirea unui polinom în numărătorul unei fracții cu un monom la numitor (pentru a obține suma integralelor nedefinite), conversia rădăcinilor în puteri, înmulțirea unui monom cu o polinom, ridicare la o putere. Aceste abilități sunt necesare pentru transformările integrandului, care ar trebui să rezulte în suma integralelor prezente în tabelul integralelor.

Găsirea împreună a integralelor nedefinite

Exemplul 1. Aflați integrala nedefinită

.

Soluţie. Vedem în numitorul integrandului un polinom în care x este pătrat. Acesta este un semn aproape sigur că puteți aplica integrala tabelului 21 (cu o arctangentă ca rezultat). Scoatem factorul doi de la numitor (există o astfel de proprietate a integralei - factorul constant poate fi scos dincolo de semnul integralei; a fost menționat mai sus ca teorema 3). Rezultatul tuturor acestor lucruri:

Acum numitorul este suma pătratelor, ceea ce înseamnă că putem aplica integrala tabelului menționată. În sfârșit obținem răspunsul:

.

Exemplul 2. Aflați integrala nedefinită

Soluţie. Aplicăm din nou teorema 3 - proprietatea integralei, pe baza căreia factorul constant poate fi scos din semnul integralei:

Aplicam formula 7 din tabelul de integrale (variabila la o putere) functiei integrand:

.

Reducem fracțiile rezultate și avem răspunsul final:

Exemplul 3. Aflați integrala nedefinită

Soluţie. Aplicând mai întâi teorema 4 și apoi teorema 3 asupra proprietăților, găsim această integrală ca sumă a trei integrale:

Toate cele trei integrale obţinute sunt tabulare. Folosim formula (7) din tabelul de integrale pentru n = 1/2, n= 2 și n= 1/5 și apoi

combină toate cele trei constante arbitrare care au fost introduse la găsirea celor trei integrale. Prin urmare, în situații similare, ar trebui introdusă o singură constantă de integrare arbitrară.

Exemplul 4. Aflați integrala nedefinită

Soluţie. Când numitorul integrandului conține un monom, putem împărți numărătorul la numitor termen cu termen. Integrala originală s-a transformat în suma a două integrale:

.

Pentru a aplica integrala tabelului, transformăm rădăcinile în puteri și iată răspunsul final:

Continuăm să găsim integrale nedefinite împreună

Exemplul 7. Aflați integrala nedefinită

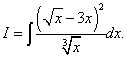
Soluţie. Dacă transformăm integralul prin pătrarea binomului și împărțirea numărătorului la numitor termen cu termen, atunci integrala inițială devine suma a trei integrale.

Cuvântul „integral” provine din latinescul integralis – integral. Acest nume a fost propus în secolul al XVII-lea. elev al marelui Leibniz (și totodată un matematician remarcabil) I. Bernoulli. Ce este o integrală în sensul modern? Mai jos vom încerca să oferim un răspuns cuprinzător la această întrebare.

Context istoric pentru apariția conceptului de integrală

La începutul secolului al XVII-lea. Oamenii de știință de frunte au luat în considerare un număr mare de probleme fizice (în primul rând mecanice) în care era necesar să se studieze dependența unor cantități de altele. Problemele cele mai evidente și stringente au fost determinarea vitezei instantanee a mișcării neuniforme a unui corp în orice moment în timp și problema inversă de a găsi distanța parcursă de corp într-o anumită perioadă de timp în timpul unei astfel de mișcări. Astăzi știm deja care este integrala vitezei de mișcare - aceasta este distanța parcursă. Dar înțelegerea modului de calcul, cunoașterea vitezei în fiecare moment, nu a apărut imediat.

La început, din luarea în considerare a unor astfel de dependențe ale mărimilor fizice, de exemplu, calea pe viteză, sa format conceptul matematic al funcției y = f(x). Studiul proprietăților diferitelor funcții a condus la nașterea analizei matematice. Oamenii de știință au căutat în mod activ modalități de a studia proprietățile diferitelor funcții.

Cum a apărut calculul integralelor și derivatelor?

După ce Descartes a creat bazele geometriei analitice și apariția capacității de a descrie grafic dependențele funcționale în axele sistemului de coordonate carteziene, cercetătorii s-au confruntat cu două noi probleme majore: cum să deseneze o tangentă la o linie curbă în orice punct și cum să găsești aria unei figuri delimitate deasupra de această curbă și linii drepte.paralele cu axele de coordonate. În mod neașteptat, s-a dovedit că primul dintre ele echivalează cu găsirea vitezei instantanee, iar al doilea echivalează cu găsirea distanței parcurse. La urma urmei, în timpul mișcării inegale, a fost reprezentat în axele de coordonate carteziene „distanță” și „timp” printr-o linie curbă.

Geniul lui Leibniz și Newton la mijlocul secolului al XVII-lea. au fost create metode care au făcut posibilă rezolvarea ambelor probleme. S-a dovedit că, pentru a desena o tangentă la o curbă într-un punct, este necesar să se găsească valoarea așa-numitei derivate a funcției care descrie această curbă în punctul său luat în considerare, iar această valoare se dovedește a fi egală. la rata de schimbare a funcției, adică în raport cu dependența „calea de viteză” însăși viteza instantanee a corpului.

Pentru a găsi aria delimitată de o linie curbă, a fost necesar să se calculeze o anumită integrală, care a dat valoarea ei exactă. Derivată și integrală sunt conceptele de bază ale calculului diferențial și integral, care stau la baza analizei matematice moderne - cea mai importantă ramură a matematicii superioare.

Zona sub o linie curbă

Deci, cum să-i determinăm valoarea exactă? Să încercăm să dezvăluim procesul de calcul prin integrală în detaliu, chiar de la bază.

Fie f o funcție continuă pe interval. Se consideră curba y = f(x), prezentată în figura de mai jos. Cum să găsiți aria regiunii delimitate de curbă), axa x și liniile x = a și x = b? Adică, zona figurii umbrite din figură.

Cel mai simplu caz este când f este o funcție constantă; adică, curba este o linie orizontală f(X) = k, unde k este constant și k ≥ 0, așa cum se arată în figura de mai jos.

În acest caz, aria de sub curbă este doar un dreptunghi cu înălțimea k și lățimea (b - a), deci aria este definită ca: k · (b - a).

Zonele altor figuri simple, cum ar fi triunghiul, trapezul și semicercul, sunt date prin formule din planimetrie.

Aria de sub orice curbă continuă y = f(x) este dată de o integrală definită, care se scrie în același mod ca o integrală obișnuită.

suma Riemann

Înainte de a aborda răspunsul detaliat la întrebarea ce este o integrală, să evidențiem câteva idei de bază.

În primul rând, aria de sub curbă este împărțită într-un anumit număr n de dungi verticale cu lățime suficient de mică Δx. În continuare, fiecare bandă verticală este înlocuită cu un dreptunghi vertical cu înălțimea f(x), lățimea Δx și aria f(x)dx. Următorul pas este formarea sumei ariilor tuturor acestor dreptunghiuri, numită suma Riemann (vezi imaginile de mai jos).

Când ne desenăm dreptunghiuri cu lățimea Δx, putem lua înălțimea lor egală cu valoarea funcției de pe marginea stângă a fiecărei benzi, adică punctele cele mai din stânga ale laturilor lor scurte superioare de lățime Δx se vor afla pe curbă. Mai mult, în secțiunea în care funcția crește și curba ei este convexă, toate dreptunghiurile sunt sub această curbă, adică suma lor va fi cu siguranță mai mică decât aria exactă de sub curba din această secțiune (a se vedea figura de mai jos). Această metodă de aproximare se numește partea stângă.

În principiu, se pot desena dreptunghiuri aproximative astfel încât punctele cele mai din dreapta ale laturilor lor scurte superioare cu lățimea Δx să se afle pe curbă. Apoi vor fi deasupra curbei, iar aproximarea zonei din această secțiune va fi mai mare decât valoarea sa exactă, așa cum se arată în figura de mai jos. Această metodă se numește dreptaci.

Dar putem lua și înălțimea fiecărui dreptunghi de aproximare, care este pur și simplu egală cu o anumită valoare a funcției într-un punct arbitrar x* i din interiorul benzii corespunzătoare Δx i (vezi figura de mai jos). În acest caz, este posibil să nu luăm nici măcar aceeași lățime a tuturor dungilor.

Să compunem suma Riemann:

Trecerea de la suma Riemann la integrala definită

În matematica superioară, se dovedește o teoremă care afirmă că dacă, cu o creștere nelimitată a numărului n de dreptunghiuri aproximate, lățimea lor cea mai mare tinde spre zero, atunci suma riemanniană A n tinde către o anumită limită A. Numărul A este la fel pentru orice metodă de formare a dreptunghiurilor aproximative și pentru orice alegere de puncte x* i .

O explicație vizuală a teoremei este dată în figura de mai jos.

Arată că, cu cât dreptunghiurile sunt mai înguste, cu atât aria figurii în trepte este mai apropiată de zona de sub curbă. Când numărul dreptunghiurilor este n→∞, lățimea lor este Δx i →0, iar limita A a sumei A n este numeric egală cu aria necesară. Această limită este integrala definită a funcției f (x):

Simbolul integral, care este o litera S italica modificată, a fost introdus de Leibniz. J. B. Fourier a sugerat punerea limitelor deasupra și sub notația integrală. Valorile de început și de sfârșit ale lui x sunt indicate clar.

Interpretarea geometrică și mecanică a integralei definite

Să încercăm să dăm un răspuns detaliat la întrebarea ce este o integrală? Să considerăm integrala pe un interval a unei funcții pozitive f(x) în interiorul acestuia și presupunem că limita superioară este mai mare decât cea inferioară a

Dacă ordonatele funcției f(x) sunt negative în interior, atunci valoarea absolută a integralei este egală cu aria dintre axa absciselor și graficul y=f(x), în timp ce integrala însăși este negativă.

În cazul unei intersecții unice sau repetate a graficului y=f(x) cu axa absciselor pe segmentul , așa cum se arată în figura de mai jos, pentru a calcula integrala este necesar să se determine diferența în care va fi minuend. egală cu suprafața totală a secțiunilor situate deasupra axei absciselor, iar subtrahendul va fi egală cu suprafața totală a parcelelor situate sub aceasta.

Deci, pentru funcția prezentată în figura de mai sus, integrala definită de la a la b va fi egală cu (S1 + S3) - (S2 + S4).

Interpretarea mecanică a integralei definite este strâns legată de cea geometrică. Să revenim la secțiunea „Suma Riemann” și să ne imaginăm că graficul prezentat în figuri exprimă funcția viteză v=f(t) pentru mișcarea neuniformă a unui punct material (axa x este axa timpului). Apoi, aria oricărui dreptunghi aproximativ cu lățimea Δt, pe care l-am construit când formăm suma Riemann, va exprima aproximativ calea punctului în timp Δt, și anume v(t*)Δt.

Suma totală a ariilor dreptunghiurilor de pe segmentul de la t 1 =a la t 2 =b va exprima aproximativ calea s în timpul t 2 - t 1, și limita acesteia, adică integrala (definită) de la a la b a funcției v = f(t ) prin dt va da valoarea exactă a căii s.

Diferenţialul unei integrale definite

Dacă revenim la desemnarea sa, atunci este foarte posibil să presupunem că a = const, iar b este o valoare specifică a unei variabile independente x. Atunci integrala definită cu o limită superioară x̃ dintr-un anumit număr se transformă într-o funcție a lui x̃. Această integrală este egală cu aria figurii de sub curbă, indicată de punctele aABb din figura de mai jos.

Cu o linie staționară aA și o dreaptă în mișcare Bb, această zonă devine o funcție a lui f(x̃), iar incrementele lui Δx̃ sunt încă reprezentate de-a lungul axei x, iar incrementele funcției f(x̃) sunt incrementele lui zona de sub curbă.

Să presupunem că am dat variabilei x̃ = b un mic increment Δx̃. Apoi, creșterea în aria figurii aABb este suma aria dreptunghiului (umbrită în figură) Bb∙Δx̃ și aria figurii BDC sub curbă. Aria dreptunghiului este egală cu Bb∙Δx̃ = f(x̃)Δx̃, adică este o funcție liniară a incrementului variabilei independente. Aria figurii BDC este evident mai mică decât aria dreptunghiului BDCK = Δx̃∙Δy, iar pe măsură ce Δx̃ →0 tinde, scade și mai repede. Aceasta înseamnă că f(x̃)Δx̃ = f(x̃)dx̃ este diferenţialul ariei variabile aABb, adică diferenţialul unei integrale definite

Din aceasta putem concluziona că calculul integralelor constă în găsirea de funcții din expresii date ale diferențialelor lor. Calculul integral este tocmai un sistem de metode pentru găsirea unor astfel de funcții folosind diferențele lor cunoscute.

Relația fundamentală a calculului integral

Ea conectează relația dintre diferențiere și integrare și arată că există o operație inversă diferențierii unei funcții - integrarea acesteia. De asemenea, arată că, dacă orice funcție f(x) este continuă, atunci prin aplicarea acestei operații matematice se poate găsi un întreg ansamblu (mulțime, mulțime) de funcții care sunt antiderivate pentru ea (sau, în caz contrar, se află integrala nedefinită a acesteia). ).

Fie funcția F(x) să desemneze rezultatul integrării funcției f(x). Corespondența dintre aceste două funcții ca urmare a integrării celei de-a doua dintre ele se notează după cum urmează:

După cum se vede, cu simbolul integral nu există limite de integrare. Aceasta înseamnă că dintr-o definită se transformă într-o integrală nedefinită. Cuvântul „nedefinit” înseamnă că rezultatul operației de integrare în acest caz nu este una, ci mai multe funcții. La urma urmei, pe lângă funcția F(x) în sine, ultimele expresii sunt satisfăcute și de orice funcție F(x)+C, unde C = const. Aceasta implică faptul că termenul constant din ansamblul de antiderivate poate fi specificat în mod arbitrar.

Trebuie subliniat că dacă integrala definită de o funcție este un număr, atunci integrala nedefinită este o funcție, sau mai precis, o mulțime a acestora. Termenul „integrare” este folosit pentru a defini operația de găsire a ambelor tipuri de integrale.

Regula de bază a integrării

Este exact opusul regulii corespunzătoare pentru diferențiere. Cum se iau integralele nedefinite? Vom analiza exemple ale acestei proceduri folosind funcții specifice.

Să ne uităm la o funcție generală de putere:

Odată ce am făcut acest lucru, fiecare termen din expresia funcției fiind integrabil (dacă există mai mult de unul), adăugăm o constantă la sfârșit. Amintiți-vă că luarea derivatei unei constante o distruge, deci luarea integralei oricărei funcții ne va oferi restabilirea acestei constante. Îl numim C pentru că constanta este necunoscută - ar putea fi orice număr! Prin urmare, putem avea un număr infinit de expresii pentru integrala nedefinită.

Să ne uităm la integrale nedefinite simple, exemple ale cărora sunt prezentate mai jos.

Să presupunem că trebuie să găsim integrala funcției:

f(x) = 4x 2 + 2x - 3.

Să începem cu primul termen. Ne uităm la exponentul lui 2 și îl creștem cu 1, apoi împărțim primul termen la exponentul rezultat al lui 3. Obținem: 4(x 3) / 3.

Apoi ne uităm la următorul membru și facem același lucru. Deoarece are un exponent de 1, exponentul rezultat va fi 2. Deci împărțim acest termen la 2: 2(x 2) / 2 = x 2.

Ultimul termen are un factor x, dar pur și simplu nu îl vedem. Ne putem gândi la ultimul termen ca (-3x 0). Aceasta este echivalentă cu (-3)∙(1). Dacă folosim regula de integrare, vom adăuga 1 la exponent pentru a-l ridica la prima putere, apoi împărțim ultimul termen la 1. Obținem 3x.

Această regulă de integrare funcționează pentru toate valorile lui n, cu excepția n = - 1 (pentru că nu putem împărți la 0).

Ne-am uitat la cel mai simplu exemplu de găsire a unei integrale. În general, rezolvarea integralelor nu este o sarcină ușoară, iar experiența acumulată deja în matematică este de un bun ajutor.

Tabele integrale

În secțiunea de mai sus, am văzut că din fiecare formulă de diferențiere se obține o formulă de integrare corespunzătoare. Prin urmare, toate opțiunile lor posibile au fost obținute de mult timp și compilate în tabele adecvate. Tabelul de integrale de mai jos conține formule pentru integrarea funcțiilor algebrice de bază. Aceste formule trebuie cunoscute pe de rost, memorându-le treptat pe măsură ce se consolidează cu exerciții.

Un alt tabel de integrale conține funcții trigonometrice de bază:

Cum se calculează o integrală definită

Se dovedește că a face asta, a ști să integrezi, adică a găsi integrale nedefinite, este foarte simplu. Și formula fondatorilor calculului integro-diferențial, Newton și Leibniz, ajută la acest lucru

Potrivit acesteia, calculul integralei dorite constă în prima etapă în găsirea nedefinitului, apoi calcularea valorii antiderivatei găsite F(x) prin substituirea x, care este mai întâi egală cu limita superioară, apoi cu cea inferioară, si, in final, determinarea diferentei acestor valori. În acest caz, constanta C nu trebuie scrisă. deoarece dispare când se efectuează scăderea.

Să ne uităm la câteva integrale cu soluții detaliate.

Să găsim aria zonei sub o sinusoidă cu jumătate de undă.

Să calculăm zona umbrită sub hiperbolă.

Să luăm acum în considerare integralele cu o soluție detaliată , folosind proprietatea aditivității în primul exemplu și înlocuirea unei variabile de integrare intermediare în al doilea. Să calculăm integrala definită a funcției raționale fracționale:

y=(1+t)/t3 de la t=1 la t=2.

Acum vom arăta cum puteți simplifica luarea integralei prin introducerea unei variabile intermediare. Să presupunem că trebuie să calculăm integrala lui (x+1) 2 .

Despre integralele improprii

Am vorbit despre integrala definită pentru un interval finit al unei funcții f(x) continuă pe ea. Dar o serie de probleme specifice duc la necesitatea extinderii conceptului de integrală în cazul în care limitele (una sau ambele) sunt egale cu infinitul, sau pentru o funcție discontinuă. De exemplu, atunci când se calculează zonele sub curbe care se apropie asimptotic de axele de coordonate. Pentru a extinde conceptul de integrală în acest caz, pe lângă trecerea la limită la calcularea sumei riemanniene a dreptunghiurilor de aproximare, se mai face un pas. Cu o astfel de trecere dublă la limită, se obține o integrală necorespunzătoare. În schimb, toate integralele discutate mai sus sunt numite proprii.

Integrale online pe site pentru elevi și școlari pentru a consolida materialul pe care l-au acoperit. De fiecare dată când începeți să rezolvați o integrală, trebuie să identificați tipul acesteia; fără aceasta, nu puteți utiliza nicio metodă, decât dacă o considerați tabelară. Nu fiecare integrală de tabel este clar vizibilă dintr-un exemplu dat; uneori trebuie să transformați funcția originală pentru a găsi antiderivată. În practică, rezolvarea integralelor se rezumă la interpretarea problemei găsirii originalului, adică a antiderivatei dintr-o familie infinită de funcții, dar dacă sunt date limitele integrării, atunci, conform formulei Newton-Leibniz, rămâne doar o singură funcție căreia trebuie aplicate calculele. În mod informal, integrala online este aria dintre graficul unei funcții și axa x în limitele integrării. Să evaluăm o integrală complexă peste o variabilă și să relaționăm răspunsul acesteia cu soluția ulterioară a problemei. Puteți, după cum se spune, să îl găsiți direct din integrand. Conform teoremei principale de analiză, integrarea este operația inversă de diferențiere, care ajută la rezolvarea ecuațiilor diferențiale. Există mai multe definiții diferite ale operațiunii de integrare, care diferă în detalii tehnice. Cu toate acestea, toate sunt compatibile, adică oricare două metode de integrare, dacă pot fi aplicate unei anumite funcții, vor da același rezultat. Cea mai simplă este integrala Riemann - aceasta este o integrală definită sau o integrală nedefinită. În mod informal, integrala unei variabile poate fi introdusă ca aria de sub grafic (figura cuprinsă între graficul funcției și axa x). Încercând să găsim această zonă, putem lua în considerare figuri formate dintr-un anumit număr de dreptunghiuri verticale, ale căror baze formează împreună un segment de integrare și se obțin prin împărțirea segmentului în numărul corespunzător de segmente mici. Calculatorul rezolvă integralele cu o descriere detaliată a acțiunilor și gratuit! O integrală nedefinită online pentru o funcție este mulțimea tuturor antiderivatelor unei funcții date. Dacă o funcție este definită și continuă pe un interval, atunci există o funcție antiderivată (sau o familie de antiderivate) pentru aceasta. Este mai bine să abordați această problemă cu atenție și să experimentați satisfacția interioară din munca depusă. Dar calcularea integralei folosind o metodă diferită de cea clasică duce uneori la rezultate neașteptate și nu trebuie să fii surprins de acest lucru. Mă bucur că acest fapt va avea o rezonanță pozitivă asupra a ceea ce se întâmplă. Lista de integrale definite și integrale nedefinite cu soluție completă detaliată pas cu pas. Găsirea online a integralei nedefinite este o problemă foarte comună în matematica superioară și în alte domenii tehnice ale științei. Metode de bază de integrare. Gândiți-vă la clădirile finalizate înainte de a găsi greșeli. Rezolvarea integralelor online - veți primi o soluție detaliată pentru diferite tipuri de integrale: nedefinite, definite, improprii. Integrala unei funcții este un analog al sumei unei șiruri. Informal vorbind, o integrală definită este aria unei părți din graficul unei funcții. Adesea, o astfel de integrală determină cât de mult este mai greu un corp decât un obiect comparabil de aceeași densitate și nu contează ce formă are, deoarece suprafața nu absoarbe apă. Fiecare student junior știe cum să găsească integrala online. Pe baza curriculum-ului școlar, se studiază și această secțiune de matematică, dar nu în detaliu, ci doar elementele de bază ale unei teme atât de complexe și importante. În majoritatea cazurilor, studenții încep să studieze integralele cu o teorie extinsă, care este, de asemenea, precedată de subiecte importante, cum ar fi derivatele și trecerea la limite - acestea sunt și limite. Rezolvarea integralelor începe treptat cu cele mai elementare exemple de funcții simple și se termină cu utilizarea multor abordări și reguli propuse în ultimul secol și chiar mult mai devreme. Calculul integral este în scop educațional în licee și școli, adică în instituțiile de învățământ secundar. Site-ul nostru web vă va ajuta întotdeauna, iar rezolvarea integralelor online va deveni obișnuită pentru dvs. și, cel mai important, o sarcină de înțeles. Pe baza acestei resurse, puteți obține cu ușurință perfecțiunea în această secțiune matematică. Înțelegând regulile pe care le studiați pas cu pas, de exemplu, integrarea pe părți sau aplicarea metodei Chebyshev, puteți rezolva cu ușurință orice test pentru numărul maxim de puncte. Deci, cum putem calcula integrala folosind binecunoscutul tabel de integrale, dar în așa fel încât soluția să fie corectă, corectă și cu cel mai precis răspuns posibil? Cum să înveți acest lucru și este posibil ca un boboc obișnuit să o facă în cel mai scurt timp posibil? Să răspundem afirmativ la această întrebare - poți! În același timp, nu numai că vei putea rezolva orice exemplu, dar vei ajunge și la nivelul unui inginer de înaltă calificare. Secretul este mai simplu ca niciodată - trebuie să depui un efort maxim și să dedici timpul necesar autopregătirii. Din păcate, nimeni nu a venit încă cu o altă cale! Dar nu totul este atât de tulbure pe cât pare la prima vedere. Dacă contactați site-ul nostru de service cu această întrebare, vă vom face viața mai ușoară, deoarece site-ul nostru poate calcula integrale online în detaliu, la o viteză foarte mare și cu un răspuns impecabil de precis. În esență, integrala nu determină modul în care raportul argumentelor afectează stabilitatea sistemului în ansamblu. Semnificația mecanică a integralei constă în multe probleme aplicate, cum ar fi determinarea volumului corpurilor și calcularea masei unui corp. În aceste calcule sunt implicate integrale triple și duble. Insistăm că rezolvarea integralelor online se realizează numai sub supravegherea profesorilor cu experiență și prin numeroase verificări.Adesea suntem întrebați despre performanța elevilor care nu frecventează cursurile, le opresc fără motiv și cum reușesc să găsească integrala în sine. Răspundem că studenții sunt oameni liberi și sunt destul de capabili să studieze în exterior, pregătindu-se pentru un test sau un examen în confortul propriei case. În câteva secunde, serviciul nostru va ajuta pe oricine să calculeze integrala oricărei funcții date pe o variabilă. Rezultatul obținut trebuie verificat luând derivata funcției antiderivative. În acest caz, constanta din soluția integralei devine zero. Această regulă se aplică în mod evident tuturor. Nu există multe site-uri care oferă un răspuns pas cu pas în câteva secunde și, cel mai important, cu precizie ridicată și într-o formă convenabilă. Dar nu trebuie să uităm cum este posibil să găsim integrala folosind un serviciu gata făcut, testat în timp și testat pe mii de exemple rezolvate online.