2 Limit zmienny. Nieskończenie mały i nieskończenie duże ilości, związek między nimi.

Granica zmiennej w pewnym momencie jest liczbowo równa temu punktowi. limx(xàa) = a

Funkcja nazywa się nieskończenie małą w punkcie, w którym xàa jeśli yà0. limf(x)_(xàa) = 0

Funkcja jest nazywana nieskończenie dużą w punkcie, w którym xàa jeśli yà0. limf(x)_(xàa) =<><>

Zależność między ilościami:

Jeśli y=Ф(х) jest nieskończenie małe, to 1/Ф(х) jest nieskończenie chore

3 Nieskończenie małe, ich główne właściwości.

Suma skończonej liczby nieskończenie małych ilości jest nieskończenie małą ilością.

Iloczyn skończonej funkcji i nieskończenie małej ilości jest nieskończenie małą ilością.

Funkcja w punkcie a ma skończoną granicę wtedy i tylko wtedy, gdy f(x) = A + U(x), gdzie U(x) jest nieskończenie małą wartością. Innym sposobem zapisania tego jest f(x) – A à 0

Porównanie funkcji nieskończenie małych:

Jeżeli granica stosunku jednego b.m. do innego b.m. równa się zero, to b.m., które było w liczniku bielszy niż wysoki porządek. Jeśli ta granica jest równa nieskończoności, to na odwrót.

A jeśli granica ich stosunku jest równa pewnej liczbie, to te b.m. tej samej kolejności.

Jeśli limit wynosi 1, to te dwa b.m. są równoważne.

Twierdzenie 1: iloczyn nieskończenie małych jest nieskończenie mały wyższego rzędu niż którykolwiek z nich.

ODA . Funkcja a (x) jest nazywana b / m, jeśli jej granica w tym t-ke wynosi 0 z tej definicji wynika z następującej właściwości funkcji b / m:

a) Suma algebraiczna i iloczyn funkcji b/m są funkcjami b/m.

b) Iloczynem funkcji b/m i funkcji ograniczonej jest funkcja b/m, tj. jeśli a(x)®0 jako x®x0, a f(x) jest zdefiniowane i ograniczone

Aby odróżnić b / m przez ich prędkość dążenia do 0, wprowadzono następujące elementy. pojęcie:

1) Jeśli stosunek 2 b/m a(x)/b(x)®0 przy x®x0, to mówią, że b/m a ma wyższy rząd wielkości niż b.

2) Jeśli a (x) / b (x) ® A¹0 z x ® x0 (liczba A), to a (x) i b (x) są nazywane b / m tego samego rzędu.

3) jeśli a(x)/b(x)®1, to a(x) i b(x) są równoważne b/m (a(x)~b(x)), dla x®x0 .

4) Jeśli a (x) / b ^ n (x) ® A¹0, to a (x) nazywamy b / m n-tego rzędu względem b (x).

Podobne definicje dla przypadków: x®x0-, x®x0+, x®-¥, x®+¥ i x®¥.

4 Granica funkcji. Podstawowe twierdzenia o granicach.

Definicja granica: niech φ(x) będzie funkcją zdefiniowaną na zbiorze X, a a będzie punktem granicznym tego zbioru. Numer A nazywa się limit funkcje dla x à a wtedy i tylko wtedy, gdy dla dowolnego e istnieje takie sąsiedztwo punktu a, że ​​|f(x) – a|< |е|

W inny sposób jest to zapisane jako f(x) à A dla x à a

Twierdzenie 1: Jeśli każdy wyraz sumy algebraicznej skończonej liczby funkcji ma granicę, ponieważ x dąży do a, to granica tej sumy algebraicznej, ponieważ x wynosi do a istnieje i jest równa tej samej sumie algebraicznej granic terminów.

Dowód: reprezentujemy funkcję jako sumę jej granicy i nieskończenie małą, dodajemy funkcje i nieskończenie małą. Okazuje się, że suma funkcji różni się od sumy granic o nieskończenie małą, co oznacza, że ​​jest to granica.

Konsekwencja: Funkcja może mieć tylko jeden limit na x rdzeni. do. Udowodniona przez sprzeczność. Okazuje się, że różnica pierwotnych funkcji zmierza do różnicy ich granic, to znaczy zero dąży do różnicy granic, a ponieważ granica funkcji stałej jest równa samej funkcji i jest unikalna, stąd otrzymujemy, że różnica w granicy wynosi 0, czyli granice są takie same.

Twierdzenie 2: Jeżeli każdy z czynników iloczynu skończonej liczby funkcji ma granicę przy x à a, to granica iloczynu przy x rdzeni do a jest równa iloczynowi granic czynników.

dowód: Rozważamy iloczyn dwóch czynników

ZMIENNE I STAŁE

W wyniku pomiaru wielkości fizyczne(czas, powierzchnia, objętość, masa, prędkość itp.) określane są ich wartości liczbowe. Matematyka zajmuje się wielkościami, abstrahując od ich specyficznej treści. W dalszej części, mówiąc o ilościach, będziemy mieli na myśli ich wartości liczbowe. W różnych zjawiskach niektóre wielkości się zmieniają, podczas gdy inne zachowują swoją wartość liczbową. Na przykład, gdy punkt porusza się jednostajnie, zmienia się czas i odległość, ale prędkość pozostaje stała.

zmienny Nazywana jest wielkość, która przyjmuje różne wartości liczbowe. Nazywa się ilość, której wartości liczbowe się nie zmieniają stały. Zmienne ilości będą oznaczone literami x, y, z,…, stały - a, b, c,…

Zauważ, że w matematyce stały często uważany za szczególny przypadek zmienna, w której wszystkie wartości liczbowe są takie same.

Zmień obszar Zmienna to suma wszystkich przyjmowanych przez nią wartości liczbowych. Obszar zmiany może składać się z jednego lub więcej przedziałów lub z jednego punktu.

ZAMÓWIONA ZMIENNA. SEKWENCJA NUMERYCZNA

Powiemy, że zmienna x jeść uporządkowana zmienna, jeśli znany jest obszar jego zmiany, a dla każdej z dwóch dowolnych jej wartości można powiedzieć, która z nich jest poprzednia, a która następna.

Szczególnym przypadkiem zmiennej uporządkowanej jest zmienna, której wartości tworzą sekwencja liczb x 1 ,x 2 ,…,x n ,… Dla takich wartości w i< j, i, j Î N , oznaczający x ja uważane za wcześniejsze, xj– kolejne, niezależnie od tego, która z tych wartości jest większa. Zatem ciąg liczbowy jest zmienną, której kolejne wartości można przenumerować. Sekwencja liczbowa będzie oznaczona przez . Poszczególne liczby ciągu nazywane są jego elementy.

Na przykład ciąg liczbowy składa się z następujących wielkości:

FUNKCJONOWAĆ

Badając różne zjawiska przyrodnicze i rozwiązując problemy techniczne, a co za tym idzie w matematyce, trzeba brać pod uwagę zmianę jednej wielkości w zależności od zmiany drugiej. Na przykład wiadomo, że pole koła wyraża się w postaci promienia wzorem S = pr2. Jeśli promień r przyjmuje różne wartości liczbowe, to obszar S przyjmuje również różne wartości liczbowe, tj. zmiana jednej zmiennej pociąga za sobą zmianę drugiej.

Jeśli każda wartość zmiennej x należący do pewnego obszaru odpowiada jednej określonej wartości innej zmiennej tak, następnie tak nazywa się funkcja zmiennej x. Symbolicznie napiszemy y=f(x). Jednocześnie zmienna x nazywa się zmienna niezależna lub argument.

Nagranie y=C, gdzie C- stała, oznacza funkcję, której wartość dla dowolnej wartości x takie same i równe C.

Wiele wartości x, dla których można wyznaczyć wartości funkcji tak zgodnie z regułą f(x), nazywa się zakres funkcji.

Zauważmy, że ciąg liczbowy jest również funkcją, której dziedzina definicji pokrywa się ze zbiorem liczb naturalnych.

Do głównych funkcji elementarnych zaliczamy wszystkie funkcje studiowane na szkolnym kursie matematyki:

elementarna funkcja jest funkcją, którą można podać za pomocą podstawowych funkcji i stałych elementarnych przy użyciu skończonej liczby operacji dodawania, odejmowania, mnożenia, dzielenia i pobierania funkcji z funkcji.

KONCEPCJA GRANICY SEKWENCJI NUMERYCZNEJ

W przyszłym kursie matematyki pojęcie granicy będzie odgrywać podstawową rolę, ponieważ podstawowe pojęcia analizy matematycznej są z nią bezpośrednio związane - pochodna, całka itp.

Zacznijmy od pojęcia granicy ciągu liczbowego.

Numer a nazywa się limit sekwencje x = {x n) jeśli dla arbitralnie przypisanej arbitralnie małej liczby dodatniej ε istnieje liczba naturalna n, że dla wszystkich n>N nierówność |x n - a|< ε.

Jeśli numer a istnieje limit sekwencji x = {x n), to mówią, że x n ma zwyczaj a, i napisz .

Aby sformułować tę definicję w terminach geometrycznych, wprowadzamy następujące pojęcie.

Sąsiedztwo punktu x 0 nazywa się arbitralnym przedziałem ( a, b) zawierający ten punkt w sobie. Często bierze się pod uwagę sąsiedztwo punktu x0, dla którego x0 jest w takim razie środkiem x0 nazywa się środek sąsiedztwo i ilość ( b–a)/2 – promień sąsiedztwo.

Dowiedzmy się więc, co pojęcie granicy ciągu liczbowego oznacza geometrycznie. W tym celu zapisujemy ostatnią nierówność z definicji w postaci

Ta nierówność oznacza, że ​​wszystkie elementy ciągu z liczbami n>N musi leżeć w przedziale (a – ε; a + ε).

Dlatego stała liczba a jest granicą ciągu liczbowego ( x n) jeśli dla dowolnej małej okolicy wyśrodkowanej w punkcie a promień ε (ε są sąsiedztwami punktu a) istnieje taki element ciągu z liczbą nże wszystkie kolejne elementy z numerami n>N będzie w tej okolicy.

Przykłady.

Zróbmy kilka uwag.

Uwaga 1. Oczywiście, jeśli wszystkie elementy ciągu liczbowego przyjmują tę samą stałą wartość xn = c, wtedy granica tej sekwencji będzie równa samej stałej. Rzeczywiście, dla każdego ε nierówność | xn-c| = |c - c| = 0 < ε.

Uwaga 2. Z definicji granicy wynika, że ​​ciąg nie może mieć dwóch granic. Załóżmy, że… x n → a i w tym samym czasie xn → b. Weź dowolne i zaznacz sąsiedztwo punktów a I b promień ε (patrz rys.). Wówczas, z definicji granicy, wszystkie elementy ciągu, zaczynając od niektórych, muszą znajdować się zarówno w sąsiedztwie punktu ale oraz w okolicach punktu b, co jest niemożliwe.

Uwaga 3. Nie należy sądzić, że każdy ciąg liczb ma granicę. Niech na przykład zmienna przyjmuje wartości . Łatwo zauważyć, że ta sekwencja nie dąży do żadnych ograniczeń.

OGRANICZENIE FUNKCJI

Niech funkcja y=f(x) określone w pewnym sąsiedztwie punktu a. Załóżmy, że zmienna niezależna x zbliża się w nieskończoność a. Oznacza to, że możemy dawać x wartości arbitralnie zbliżone do a ale nie równe a. Oznaczmy to w ten sposób x → a. Dla takiego x znajdź odpowiednie wartości funkcji. Może się zdarzyć, że wartości f(x) też zbliża się w nieskończoność do jakiejś liczby b.Wtedy mówią, że liczba b istnieje ograniczenie funkcji f(x) w x → a.

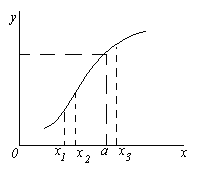
Wprowadźmy ścisłą definicję granicy funkcji.

Funkcjonować y=f(x) dąży do granicy b jako x → a, jeśli dla każdej liczby dodatniej ε, nieważne jak mała jest, można podać liczbę dodatnią δ taką, że dla wszystkich x ≠ a z dziedziny funkcji spełniających nierówność | x-a| < δ, имеет место неравенство |f(x) - b| < ε. Если b istnieje ograniczenie funkcji f(x) w x → a, następnie napisz lub f(x) → b w x → a.

Tę definicję ilustrujemy na wykresie funkcji. Dlatego z nierówności | x-a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при x Î ( a - δ, a+ δ) odpowiednie wartości funkcji f(x) Î ( b - ε, b+ ε), to przyjmując dowolne ε > 0, możemy wybrać liczbę δ taką, że dla wszystkich punktów x, leżące w δ, sąsiedztwie punktu a, odpowiednie punkty wykresu funkcji muszą leżeć wewnątrz pasa o szerokości 2ε ograniczonego liniami prostymi y=b– ε i y=b + ε.

Łatwo zauważyć, że granica funkcji musi mieć te same właściwości, co granica ciągu liczbowego, a mianowicie, jeśli dla x → a funkcja ma limit, to jest unikalna.

Przykłady.

KONCEPCJA GRANICY FUNKCJI W PUNKCIE MIĘDZYNARODOWYM

Do tej pory rozważaliśmy granice dla przypadku, gdy zmienna x dążył do pewnej stałej liczby.

Powiemy, że zmienna x dąży do nieskończoności, jeśli dla każdej określonej liczby dodatniej m(może być dowolnie duża) możesz podać taką wartość x=x 0, począwszy od którego wszystkie kolejne wartości zmiennej będą spełniały nierówność |x|>M.

Na przykład niech zmienna x przyjmuje wartości x 1 = –1, x 2 = 2, x 3 = –3, …, x n=(–1) n n, … Jasne jest, że jest to zmienna nieskończenie duża, ponieważ dla wszystkich m> 0, wszystkie wartości zmiennej, począwszy od niektórych, będą większe w wartości bezwzględnej m.

zmienny x → +∞, jeśli za arbitralnie m> 0, wszystkie kolejne wartości zmiennej, począwszy od pewnej, spełniają nierówność x > M.

Podobnie, x→ – ∞, jeśli w ogóle m > 0 x< -M .

Powiemy, że funkcja f(x) dąży do granic b w x→ ∞ jeśli dla dowolnej małej liczby dodatniej ε można znaleźć taką liczbę dodatnią m, który dla wszystkich wartości x zaspokojenie nierówności |x|>M, nierówność | f(x) - b| < ε.

Wyznaczyć .

Przykłady.

NIESKOŃCZONE WIELKIE FUNKCJE

Wcześniej rozważaliśmy przypadki, w których funkcja f(x) dążenie do jakiegoś ostatecznego limitu b w x → a lub x → ∞.

Rozważmy teraz przypadek, gdy funkcja y=f(x) jakiś sposób na zmianę argumentacji.

Funkcjonować f(x) dąży do nieskończoności, jak x → a, tj. jest nieskończenie duży wartość, jeśli dla dowolnej liczby m, jakkolwiek by ona była duża, można znaleźć δ > 0 takie, że dla wszystkich wartości x≠a, spełniający warunek | x-a| < δ, имеет место неравенство |f(x)| > m.

Jeśli f(x) dąży do nieskończoności, jak x→a, następnie napisz lub f(x)→∞ w x→a.

Sformułuj podobną definicję dla przypadku, gdy x→∞.

Jeśli f(x) dąży do nieskończoności, jak x→a a jednocześnie przyjmuje tylko wartości dodatnie lub tylko ujemne, odpowiednio napisz lub .

Przykłady.

FUNKCJE OGRANICZONE

Niech funkcja y=f(x), zdefiniowany na pewnym zestawie D wartości argumentów.

Funkcjonować y=f(x) nazywa się ograniczony na planie D jeśli jest liczba dodatnia m tak, że dla wszystkich wartości x z rozważanego zbioru nierówności |f(x)|≤M. Jeśli taka liczba m nie istnieje, to funkcja f(x) nazywa się bez limitu na planie D.

Przykłady.

1. Funkcjonować tak= grzech x, zdefiniowany w -∞<x<+∞, является ограниченной, так как при всех значениях x|grzech x|≤1 = m.
2. Funkcjonować tak=x 2 +2 jest ograniczone np. do przedziału , ponieważ dla wszystkich x z tej sekcji |f(x)| ≤f(3) = 11.
3. Rozważ funkcję tak=ln x w xн (0; 1). Ta funkcja jest nieograniczona we wskazanym segmencie, ponieważ dla x→0 log x→-∞.

Funkcjonować y=f(x) nazywa się ograniczone jako x → a jeśli istnieje dzielnica wyśrodkowana w punkcie ale gdzie funkcja jest ograniczona.

Funkcjonować y=f(x) nazywa się ograniczone jako x→∞ jeśli jest taka liczba N> 0, co dla wszystkich wartości x |x|>N, funkcja f(x) ograniczony.

Ustalmy połączenie między funkcją ograniczoną a funkcją, która ma granicę.

Twierdzenie 1. Jeśli i b jest liczbą skończoną, to funkcja f(x) ograniczone w x→a.

Dowód. Dlatego , to dla dowolnego ε>0 istnieje liczba δ>0 taka, że ​​dla wszystkich wartości x zaspokojenie nierówności |x-a|< δ, nierówność |f(x) –b|< ε. Korzystanie z właściwości modułu |f(x) – b|≥|f(x)| - |b|, ostatnią nierówność zapisujemy w postaci |f(x)|<|b|+ ε. Tak więc, jeśli umieścimy M=|b|+ε, to x→a |f(x)|

Komentarz. Z definicji funkcji ograniczonej wynika, że ​​jeśli , to jest nieograniczona. Jednak odwrotność nie jest prawdziwa: funkcja nieograniczona może nie być nieskończenie duża. Daj przykład.

Twierdzenie 2. Jeśli , to funkcja y=1/f(x) ograniczone w x→a.

Dowód. Z warunków twierdzenia wynika, że ​​dla dowolnego ε>0, w pewnym sąsiedztwie punktu a mamy |f(x) – b|< ε. Dlatego |f(x) – b|=|b – f(x)| ≥|b| - |f(x)|, następnie |b| - |f(x)|< ε. W konsekwencji, |f(x)|>|b| -ε >0. Dlatego

Strona główna > Dokument

LIMIT. CIĄGŁOŚĆ FUNKCJI

ZMIENNE I STAŁE W wyniku pomiaru wielkości fizycznych (czas, powierzchnia, objętość, masa, prędkość itp.) określane są ich wartości liczbowe. Matematyka zajmuje się wielkościami, abstrahując od ich specyficznej treści. W dalszej części, mówiąc o ilościach, będziemy mieli na myśli ich wartości liczbowe. W różnych zjawiskach niektóre wielkości się zmieniają, podczas gdy inne zachowują swoją wartość liczbową. Na przykład, gdy punkt porusza się jednostajnie, zmienia się czas i odległość, ale prędkość pozostaje stała. zmienny Nazywana jest wielkość, która przyjmuje różne wartości liczbowe. Nazywa się ilość, której wartości liczbowe się nie zmieniają stały. Zmienne ilości będą oznaczone literami x, y, z,…, stały - a, b, c,… Zauważ, że w matematyce stała wartość jest często uważana za szczególny przypadek zmiennej, w której wszystkie wartości liczbowe są takie same. Zmień obszar Zmienna to suma wszystkich przyjmowanych przez nią wartości liczbowych. Obszar zmiany może składać się z jednego lub więcej przedziałów lub z jednego punktu. ZAMÓWIONA ZMIENNA. SEKWENCJA NUMERYCZNA Powiemy, że zmienna x jeść uporządkowana zmienna, jeśli znany jest obszar jego zmiany, a dla każdej z dwóch dowolnych jej wartości można powiedzieć, która z nich jest poprzednia, a która następna. Szczególnym przypadkiem zmiennej uporządkowanej jest zmienna, której wartości tworzą sekwencja liczb x 1 ,x 2 ,…,x n ,… Dla takich wartości w i< j, i, j Î N , oznaczający x i uważane za wcześniejsze, x J– kolejne, niezależnie od tego, która z tych wartości jest większa. Zatem ciąg liczbowy jest zmienną, której kolejne wartości można przenumerować. Sekwencja liczbowa będzie oznaczona przez . Poszczególne liczby ciągu nazywane są jego elementy. Na przykład ciąg liczbowy składa się z następujących wielkości: FUNKCJONOWAĆ Badając różne zjawiska przyrodnicze i rozwiązując problemy techniczne, a co za tym idzie w matematyce, trzeba brać pod uwagę zmianę jednej wielkości w zależności od zmiany drugiej. Na przykład wiadomo, że pole koła wyraża się w postaci promienia wzorem S = pr 2 . Jeśli promień r przyjmuje różne wartości liczbowe, to obszar S przyjmuje również różne wartości liczbowe, tj. zmiana jednej zmiennej pociąga za sobą zmianę drugiej. Jeśli każda wartość zmiennej x należący do pewnego obszaru odpowiada jednej określonej wartości innej zmiennej tak, następnie tak nazywa się funkcja zmiennej x. Symbolicznie napiszemy y=f(x). Jednocześnie zmienna x nazywa się zmienna niezależna lub argument. Nagranie y=C, gdzie C- stała, oznacza funkcję, której wartość dla dowolnej wartości x takie same i równe C. Wiele wartości x, dla których można wyznaczyć wartości funkcji tak zgodnie z regułą f(x), nazywa się zakres funkcji. Zauważmy, że ciąg liczbowy jest również funkcją, której dziedzina definicji pokrywa się ze zbiorem liczb naturalnych. Do głównych funkcji elementarnych zaliczamy wszystkie funkcje studiowane na szkolnym kursie matematyki: elementarna funkcja jest funkcją, którą można podać za pomocą podstawowych funkcji i stałych elementarnych przy użyciu skończonej liczby operacji dodawania, odejmowania, mnożenia, dzielenia i pobierania funkcji z funkcji. KONCEPCJA GRANICY SEKWENCJI NUMERYCZNEJ W przyszłym kursie matematyki pojęcie granicy będzie odgrywać podstawową rolę, ponieważ podstawowe pojęcia analizy matematycznej są z nią bezpośrednio związane - pochodna, całka itp. Zacznijmy od pojęcia granicy ciągu liczbowego. Numer a nazywa się limit sekwencje x = {x n) jeśli dla arbitralnie przypisanej arbitralnie małej liczby dodatniej ε istnieje liczba naturalna n, że dla wszystkich n>N nierówność |x n - a|< ε. Если число a istnieje limit sekwencji x = {x n), to mówią, że x n ma zwyczaj a, i napisz . Aby sformułować tę definicję w terminach geometrycznych, wprowadzamy następujące pojęcie. Sąsiedztwo punktu x 0 nazywa się arbitralnym przedziałem ( a, b) zawierający ten punkt w sobie. Często bierze się pod uwagę sąsiedztwo punktu x 0 , dla którego x 0 jest w takim razie środkiem x 0 nazywa się środek sąsiedztwo i ilość ( b–a)/2 – promień sąsiedztwo. Dowiedzmy się więc, co pojęcie granicy ciągu liczbowego oznacza geometrycznie. W tym celu zapisujemy ostatnią nierówność z definicji w postaci

Ta nierówność oznacza, że ​​wszystkie elementy ciągu z liczbami n>N musi leżeć w przedziale (a – ε; a + ε). OD dlatego stała liczba a jest granicą ciągu liczbowego ( x n) jeśli dla dowolnej małej okolicy wyśrodkowanej w punkcie a promień ε (ε są sąsiedztwami punktu a) istnieje taki element ciągu z liczbą nże wszystkie kolejne elementy z numerami n>N będzie w tej okolicy. Przykłady.

Niech zmienna x przyjmuje wartości sekwencyjnie

Udowodnijmy, że granica tego ciągu liczbowego jest równa 1. Weźmy dowolną liczbę dodatnią ε. Musimy znaleźć taką liczbę naturalną n, że dla wszystkich n>N nierówność | x n - 1| < ε. Действительно, т.к. , to do spełnienia relacji |x n - a|< ε достаточно, чтобы или . Поэтому, взяв в качестве n dowolna liczba naturalna, która spełnia nierówność , otrzymujemy to, czego potrzebujemy. Jeśli więc weźmiemy na przykład , to ustawienie N= 6, dla wszystkich n>6 będziemy mieli . Weź dowolne ε > 0. Rozważ . Wtedy , jeśli lub , tj. . Dlatego wybieramy dowolną liczbę naturalną, która spełnia nierówność . Zróbmy kilka uwag. Uwaga 1. Oczywiście, jeśli wszystkie elementy ciągu liczbowego przyjmują tę samą stałą wartość x n = c, wtedy granica tej sekwencji będzie równa samej stałej. Rzeczywiście, dla każdego ε nierówność | x n -C| = |c - c| = 0 < ε. Z uwaga 2. Z definicji granicy wynika, że ​​ciąg nie może mieć dwóch granic. Załóżmy, że… x n → a i w tym samym czasie x n →b. Weź dowolne i zaznacz sąsiedztwo punktów a I b promień ε (patrz rys.). Wówczas, z definicji granicy, wszystkie elementy ciągu, zaczynając od niektórych, muszą znajdować się zarówno w sąsiedztwie punktu ale oraz w okolicach punktu b, co jest niemożliwe. Uwaga 3. Nie należy sądzić, że każdy ciąg liczb ma granicę. Niech na przykład zmienna przyjmuje wartości . Łatwo zauważyć, że ta sekwencja nie dąży do żadnych ograniczeń.

OGRANICZENIE FUNKCJI Niech funkcja y=f(x) określone w pewnym sąsiedztwie punktu a. Załóżmy, że zmienna niezależna x zbliża się w nieskończoność a. Oznacza to, że możemy dawać x wartości arbitralnie zbliżone do a ale nie równe a. Oznaczmy to w ten sposób x → a. Dla takiego x znajdź odpowiednie wartości funkcji. Może się zdarzyć, że wartości f(x) też zbliża się w nieskończoność do jakiejś liczby b.Wtedy mówią, że liczba b istnieje ograniczenie funkcji f(x) w x → a. Wprowadźmy ścisłą definicję granicy funkcji. Funkcjonować y=f(x) dąży do granicy b jako x → a, jeśli dla każdej liczby dodatniej ε, nieważne jak mała jest, można podać liczbę dodatnią δ taką, że dla wszystkich x ≠ a z dziedziny funkcji | x-a| < δ, имеет место неравенство |f(x) - b| < ε. Если b istnieje ograniczenie funkcji f(x) w x → a, następnie napisz lub f(x) → b w x → a. Tę definicję ilustrujemy na wykresie funkcji. Dlatego z nierówności | x-a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при x Î ( a - δ, a+ δ) odpowiednie wartości funkcji f(x) Î ( b - ε, b+ ε), to przyjmując dowolne ε > 0, możemy wybrać liczbę δ taką, że dla wszystkich punktów x, leżący w δ, sąsiedztwie punktu a, odpowiednie punkty wykresu funkcji muszą leżeć wewnątrz pasa o szerokości 2ε ograniczonego liniami prostymi y=b– ε i y=b+ mi. Łatwo zauważyć, że granica funkcji musi mieć te same właściwości, co granica ciągu liczbowego, a mianowicie, jeśli dla x → a funkcja ma limit, to jest unikalna. Przykłady. Korzystając z wykresu danej funkcji łatwo zauważyć, że .

KONCEPCJA GRANICY FUNKCJI W NIESKOŃCZO ODLEGŁYM MIEJSCU Do tej pory rozważaliśmy granice dla przypadku, gdy zmienna x dążył do pewnej stałej liczby. Powiemy, że zmienna x dąży do nieskończoności, jeśli dla każdej określonej liczby dodatniej m(może być dowolnie duża) możesz podać taką wartość x=x 0 , począwszy od którego wszystkie kolejne wartości zmiennej będą spełniały nierówność |x|>M. Na przykład niech zmienna x przyjmuje wartości x 1 = –1, x 2 = 2, x 3 = –3, …, x n=(–1) n n, … Jasne jest, że jest to zmienna nieskończenie duża, ponieważ dla wszystkich m> 0, wszystkie wartości zmiennej, począwszy od niektórych, będą większe w wartości bezwzględnej m. zmienny x → +∞, jeśli za arbitralnie m> 0, wszystkie kolejne wartości zmiennej, począwszy od pewnej, spełniają nierówność x > M. Podobnie, x→ – ∞, jeśli w ogóle m > 0 x< -M . Powiemy, że funkcja f(x) dąży do granic b w x→ ∞ jeśli dla dowolnej małej liczby dodatniej ε można znaleźć taką liczbę dodatnią m, który dla wszystkich wartości x zaspokojenie nierówności |x|>M, nierówność | f(x) - b| < ε. Обозначают . Przykłady. h Konieczne jest udowodnienie, że dla dowolnego ε nierówność utrzyma się, gdy |x|>M, a liczba m musi być określona przez wybór ε. Zapisana nierówność jest równoważna poniższej, która będzie obowiązywać, jeśli |x|> 1/ε=M. Oznacza to, że (patrz rys.). NIESKOŃCZONE WIELKIE FUNKCJE Wcześniej rozważaliśmy przypadki, w których funkcja f(x) dążenie do jakiegoś ostatecznego limitu b w x → a lub x→∞. Rozważmy teraz przypadek, gdy funkcja y=f(x) jakiś sposób na zmianę argumentacji. Funkcjonować f(x) dąży do nieskończoności, jak x → a, tj. jest nieskończenie duży wartość, jeśli dla dowolnej liczby m, jakkolwiek by ona była duża, można znaleźć δ > 0 takie, że dla wszystkich wartości x≠a, spełniający warunek | x-a| < δ, имеет место неравенство |f(x)| > m. Jeśli f(x) dąży do nieskończoności, jak x→a, następnie napisz lub f(x)→∞ w x→a. Sformułuj podobną definicję dla przypadku, gdy x→∞. Jeśli f(x) dąży do nieskończoności, jak x→a a jednocześnie przyjmuje tylko wartości dodatnie lub tylko ujemne, odpowiednio napisz lub . Przykłady. FUNKCJE OGRANICZONE Niech funkcja y=f(x), zdefiniowany na pewnym zestawie D wartości argumentów. Funkcjonować y=f(x) nazywa się ograniczony na planie D jeśli jest liczba dodatnia m tak, że dla wszystkich wartości x z rozważanego zbioru nierówności |f(x)|≤M. Jeśli taka liczba m nie istnieje, to funkcja f(x) nazywa się bez limitu na planie D. Przykłady.

Funkcjonować tak= grzech x, zdefiniowany w -∞<x<+∞, является ограниченной, так как при всех значениях x|grzech x|≤1 = m. Funkcjonować tak=x 2 +2 jest ograniczone np. do przedziału , ponieważ dla wszystkich x z tej sekcji |f(x)| ≤f(3) = 11. Rozważ funkcję tak=ln x w xн (0; 1). Ta funkcja jest nieograniczona we wskazanym segmencie, ponieważ dla x→0 log x→-∞.

Funkcjonować y=f(x) nazywa się ograniczone jako x → a jeśli istnieje dzielnica wyśrodkowana w punkcie ale gdzie funkcja jest ograniczona. Funkcjonować y=f(x) nazywa się ograniczone jako x→∞ jeśli jest taka liczba N> 0, co dla wszystkich wartości x zaspokojenie nierówności |x|>N, funkcja f(x) ograniczony. Ustalmy połączenie między funkcją ograniczoną a funkcją, która ma granicę. Twierdzenie 1. Jeśli i b jest liczbą skończoną, to funkcja f(x) ograniczone w x→a. Dowód. Dlatego , to dla dowolnego ε>0 istnieje liczba δ>0 taka, że ​​dla wszystkich wartości x zaspokojenie nierówności |x-a|< δ, nierówność |f(x) –b|< ε. Korzystanie z właściwości modułu |f(x) – b|≥|f(x)| - |b|, ostatnią nierówność zapisujemy w postaci |f(x)|<|b|+ ε. Tak więc, jeśli umieścimy M=|b|+ε, to x→a |f(x)| Komentarz. Z definicji funkcji ograniczonej wynika, że ​​jeśli , to jest nieograniczona. Jednak odwrotność nie jest prawdziwa: funkcja nieograniczona może nie być nieskończenie duża. Daj przykład. Twierdzenie 2. Jeśli , to funkcja y=1/f(x) ograniczone w x→a. Dowód. Z warunków twierdzenia wynika, że ​​dla dowolnego ε>0, w pewnym sąsiedztwie punktu a mamy |f(x) – b|< ε. Dlatego |f(x) – b|=|b – f(x)| ≥|b| - |f(x)|, następnie |b| - |f(x)|< ε. W konsekwencji, |f(x)|>|b| -ε >0. Dlatego .

NIESKOŃCZONIE DUŻE I NIESKOŃCZO MAŁE FUNKCJE

NIESKOŃCZONE MAŁE FUNKCJE I ICH GŁÓWNE WŁAŚCIWOŚCI Funkcjonować y=f(x) nazywa się nieskończenie mały w x→a albo kiedy x→∞ jeśli lub , tj. Funkcja nieskończenie mała to funkcja, której granica w danym punkcie wynosi zero. P przykłady. Ustalmy następującą ważną relację: Twierdzenie. Jeśli funkcja y=f(x) reprezentowalne w x→a jako suma stałej liczby b i nieskończenie małe α(x): f(x)=b+ α(x) następnie . I odwrotnie, jeśli , to f(x)=b+α(x), gdzie topór) jest nieskończenie mały w x→a. Dowód. Rozważmy główne własności funkcji nieskończenie małych. Twierdzenie 1. Suma algebraiczna dwóch, trzech i ogólnie dowolna skończona liczba nieskończenie małych jest funkcją nieskończenie małą. Dowód. Dajmy dowód dla dwóch terminów. Zostawiać f(x)=α(x)+β(x), gdzie i . Musimy udowodnić, że dla arbitralnie arbitralnie małych ε > 0 tam δ> 0, tak, że dla x zaspokojenie nierówności |x – a|<δ , wykonywane |f(x)|< ε. W ten sposób ustalamy dowolną liczbę ε > 0. Ponieważ zgodnie z hipotezą twierdzenia, α(x) jest funkcją nieskończenie małą, to istnieje δ 1 > 0, co w |x – a|< δ 1 mamy |α(x)|< ε / 2. Podobnie, ponieważ β(x) jest nieskończenie małe, to jest takie δ 2 > 0, co w |x – a|< δ 2 mamy | β(x)|< ε / 2. Weźmy δ=min(δ1 , δ2 } .Wtedy w sąsiedztwie punktu a promień δ każda z nierówności zostanie zaspokojona |α(x)|< ε / 2 i | β(x)|< ε / 2. Dlatego w tej okolicy będzie |f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε, tj. |f(x)|< ε, co miało zostać udowodnione. Twierdzenie 2. Iloczyn funkcji nieskończenie małej topór) dla ograniczonej funkcji f(x) w x→a(albo kiedy x→∞) jest funkcją nieskończenie małą. Dowód. Ponieważ funkcja f(x) jest ograniczona, to jest liczba m tak, że dla wszystkich wartości x z jakiejś okolicy punktu a|f(x)|≤M. Ponadto, ponieważ topór) jest nieskończenie małą funkcją dla x→a, to dla dowolnego ε > 0 jest sąsiedztwo punktu a, w którym nierówności |α(x)|< ε /M. Następnie w mniejszej z tych dzielnic mamy | αf|< ε /M= ε. A to oznacza, że af- nieskończenie mały. Z okazji x→∞ dowód jest przeprowadzany w podobny sposób. Z udowodnionego twierdzenia wynika: Konsekwencja 1. Jeśli i , to . Konsekwencja 2. Jeśli i c= const, to . Twierdzenie 3. Stosunek nieskończenie małej funkcji α(x) na funkcję f(x), którego granica jest niezerowa, jest funkcją nieskończenie małą. Dowód. Zostawiać . Wtedy 1 /f(x) istnieje ograniczona funkcja. Dlatego ułamek jest iloczynem funkcji nieskończenie małej i funkcji ograniczonej, tj. funkcja jest nieskończenie mała.

1. 1. Ogólne kulturowe i praktyczne znaczenie paradygmatu ciągłości oraz rachunku różniczkowego i całkowego

   abstrakcyjny

   Załącznik nr 1 Elementy zastosowania matematyki w badaniach społeczno-gospodarczych i społeczno-menedżerskich oraz we współczesnej praktyce gospodarczej - możliwe tematy aplikacyjne abstraktów,

2. Dokument

   W tym rozdziale opisano prawidłowe nazwy zmiennych i funkcji programu Mathcad, predefiniowane zmienne, takie jak te, oraz reprezentacje liczb. Mathcad obsługuje liczby zespolone tak samo łatwo, jak liczby rzeczywiste.

3. „Funkcje i wykresy”

   abstrakcyjny

   Chciałbym dowiedzieć się więcej o funkcji i wykresach funkcji. Od 7 klasy uczymy się algebry według programu A.G. Mordkowicza. Uważam, że pojęcie zależności funkcjonalnej jest jednym z centralnych pojęć w matematyce i przenika wszystkie jej zastosowania.

4. Krótki przegląd i instrukcja obsługi. Książka jest pierwszym tego rodzaju przeglądem i podręcznikiem dotyczącym wirtualnej fizyki i jest przeznaczona dla szerokiego grona czytelników zainteresowanych problematyką nauki w ogóle, a fizyką w szczególności.

   Książka

   Książka jest pierwszym tego rodzaju przeglądem i podręcznikiem dotyczącym wirtualnej fizyki i jest przeznaczona dla szerokiego grona czytelników zainteresowanych problematyką nauki w ogóle, a fizyką w szczególności.

5. Program egzaminów wstępnych do magistratu na kierunku 010200. 68 Matematyka. Matematyka stosowana „Analiza matematyczna”

   Program

   Granica ciągu liczbowego. Główne właściwości: unikalność limitu; ograniczoność ciągu zbieżnego; zbieżność podciągu ciągu zbieżnego.

Niech x będzie zmienną uporządkowaną (na przykład ciągiem liczbowym).

Definicja.

stała liczbaanazywa się granicą zmiennej x, jeśli dowolna arbitralnie mała liczba dodatnia nie braliśmy, można podać taką wartość zmiennej x, aby wszystkie kolejne wartości zmiennej spełniały nierówność x-ale .

Symbolicznie zapisuje się to xa lub limx = a (z łac. limes – granica).

Geometrycznie ta definicja oznacza, że ​​bez względu na to, jak małe  - sąsiedztwo punktu a przyjmiemy, wszystkie kolejne wartości x po pewnym czasie będą leżeć w tym sąsiedztwie.

Z rysunku widać, że nierówności
oznacza, że ​​odległość od punktu x do a jest mniejsza niż . A to jest wnętrze okolicy. Punkt x oczywiście spełnia podwójną nierówność a- i są równoważne.

O definicja: Dla ciągu liczbowego (x n ) a jest granicą, jeśli zgodnie z
możesz podać liczbęN taką, że dla wszystkich

W przypadku elementów sekwencji wszystkie wartości x N , x N +1 i poza leżą wewnątrz - Sąsiedztwo jest koniecznością.

Zmienna x, której wartości tworzą ciąg liczbowy x 1 ,x 2 ,…,x n jest często zapisywana jako element ciągu x=x n lub (x n ). Na przykład (1/n). Jest to zmienna lub sekwencja ze wspólnym wyrazem x n = 1/n: 1.1/2.1/3…

Przykład: Niech zmienna x przyjmie kolejne wartości: x 1 =2/1, x 2 =3/2, x 3 =4/3, …,x n =(n+1)/n,… tj. tworzą sekwencję liczb. Udowodnijmy, że
.

Weźmy
.


. Jak tylko liczba stanie się
, przyjmiemy to jako N. Wtedy nierówność utrzyma się przez
. Ale wtedy wszystko jest udowodnione.

Twierdzenie 1: granica stałej jest równa tej stałej. Dowód: Wartość stała to szczególny przypadek zmiennej - wszystkie jej wartości \u003d c: x \u003d c / Ale wtedy limc \u003d c.

Twierdzenie 2: Zmienna x nie może mieć dwóch granic.

Dowód: Powiedzmy, że limx=a i limx=b. Następnie

I
po pewnej wartości x. Ale wtedy

Dlatego dowolnie mała, to nierówność jest możliwa tylko dla a=b

Notatka: Zmienna może nie mieć limitu: x=x n =(-1) n =-1,+1,-1,+1. Odległość do dowolnego punktu a od jego wartości –1,+1 nie może być mniejsza niż 1/2
(-1) n nie ma granic.

Przyjęliśmy, że a jest liczbą. Ale zmienna x może również dążyć do nieskończoności.

Definicja: Zmienna x dąży do nieskończoności, jeśli for
zaczynając od pewnej wartości x, pozostałe wartości zaspokajają nierówność
. Zmienna x ma tendencję do
, jeśli w tych samych warunkach nierówność x>M jest spełniona i k - , jeśli w tych samych warunkach nierówność x<-M. Если переменная X стремится к бесконечности, то её называют nieskończenie duży i napisz

Przykład: x=xn=n2. Weźmy
>0. Należy wykonać n 2 >M. n>
. Gdy tylko n spełnia tę nierówność, to dla wszystkich x n = n 2 nierówność zachodzi. Więc n 2
, a raczej n 2
.

§3. Granica funkcji.

Założymy, że argument x funkcji y=f(x) dąży do x 0 lub .

Rozważ zachowanie funkcji y w takich przypadkach.

Definicja.

Niech funkcja y=f(x) będzie zdefiniowana w jakimś sąsiedztwie punktu x 0 . Liczbę A nazywamy granicą funkcji w xx 0, jeśli dla dowolnego , dowolnie małej, można określić taką liczbę , że dla wszystkich xx 0 i spełniających nierówność xx 0   nierówność f(x)-A.

Jeśli A jest granicą funkcji f(x), to piszemy
lub f(x)A w xx 0.

O Definicję można zilustrować w ten sposób geometrycznie.

Jeśli A jest granicą f (x) w xx 0, to biorąc dowolne -sąsiedztwo punktu A, zawsze możemy wskazać takie  - sąsiedztwo punktu x 0, że dla wszystkich x z tego  - sąsiedztw wartości funkcji f (x) są oddzielone od A nie dalej niż , tj. wpaść w wybrane -sąsiedztwo punktu A, lub w każdym razie część grafu odpowiadająca punktom x z -sąsiedztwa leży w całości w pasie o szerokości 2.

Widać, że im mniejsze , tym mniejsze powinno być .

Definicja.

Niech argument x dąży do punktu x 0, przyjmując przez cały czas wartości xx 0 xx 0  Następnie liczba A 1 (A 2), do której dąży funkcja f (x), nazywamy granicą funkcji f (x) w punkcie x 0 po prawej (lewo) lub prawoskrętnej (lewoskrętnej).

Jest napisane: lim x  x0 + 0 f (x) \u003d A 1, (lim x  x0-0 f (x) \u003d A 2).

Można wykazać, że jeśli istnieje granica lim x  x0 f(x)=A, to obie granice jednostronne istnieją w tym punkcie i są sobie równe, A 1 =A 2 =A. I odwrotnie: jeśli istnieją jednostronne limity i są one równe, to istnieje wspólny limit. Jeśli co najmniej jeden nie istnieje lub nie są równe, to granica funkcji nie istnieje.

Przykład.

Udowodnij, że f(x)=3x-2 ma granicę x1 równą 1.

Dowolna 3.

Jako  możesz wziąć dowolne liczby dodatnie /3; 0</3.

Udowodniliśmy, że dla dowolnego  wystarczy przyjąć /3 tak, że od 0х f(х)-1, ale to oznacza, że ​​lim X  (3x-2)=1.

Definicja.

h
słowo A nazywamy granicą funkcji y=f(x) przy x, jeśli dla dowolnego  (dowolnie małego) można podać liczbę dodatnią P taką, że dla wszystkich wartości x spełniających nierówność х P nierówność  f(x)-A.

Napisz lim x  f(x)=A.

Geometrycznie oznacza to, że dla dowolnego  wykres funkcji dla xp i x-p znajduje się w pasku o szerokości 2.

Przykład.

f(x)=1/x w x, f(x)0.

Niezależnie od przyjętego 0, wykres funkcji w xP i x-P będzie znajdował się w pasku o szerokości 2.

1/х, 1/х, x1/, Р=1/.

Podobnie są zdefiniowane i
f(x)=A 1 i
f (x) \u003d A 2. W pierwszym przypadku nierówność f(x)-A 1  dla xP musi być spełniona, w drugim przypadku f(x)-A 2  dla x-P (P0 .

Więc,
1/x=0, oraz
1/x=0. Ich równość pozwala nam wziąć pod uwagę ogólną granicę
1/x=0.

Spośród różnych sposobów zachowania zmiennych najważniejszy jest ten, w którym zmienna dąży do pewnej granicy. W tym przypadku wartości przyjmowane przez zmienną x, zbliżyć się dowolnie do jakiejś stałej liczby a- limit tej zmiennej. Mówi się, że zmienna dąży w nieskończoność do stałej liczby ale(do twojego limitu). Podajmy bardziej szczegółowo odpowiednią definicję.

Zmienna x dąży do granicy a (a - stała liczba) jeśli wartość bezwzględna różnica między x i a staje się arbitralnie mała w procesie zmiany zmiennej.

Innymi słowy, tę samą definicję można powiedzieć.

Definicja.Stała liczba a nazywa sięzmienny limitx jeśli - wartość bezwzględna różnicy między x i a staje się dowolnie mała w procesie zmiany zmiennej x.

Fakt, że liczba ale, jest granicą zmiennej, zapisuje się w następujący sposób:

( - pierwsze litery słowa limes - limit) lub x-> a

Wyjaśnijmy, co należy rozumieć przez słowa „wartość staje się dowolnie mała”, które są dostępne w definicji granicy. Przyjmijmy więc dowolną liczbę dodatnią , jeśli, począwszy od pewnego momentu zmiany zmiennej X, wartości staną się i staną się mniejsze niż to .

Zmienna dąży do granicy, jeśli jest dodatnia. począwszy od pewnego momentu zmiany zmiennej , nierówność jest spełniona .

Definicja granicy ma proste znaczenie geometryczne: nierówność oznacza, że ​​znajduje się w -sąsiedztwie punktu , tj. w przedziale (ryc. 26). Zatem definicja granicy w formie geometrycznej to: liczba jest granicą zmiennej jeśli dla dowolnego (arbitralnie mała)-sąsiedztwo punktu możesz określić taki moment w zmianie zmiennej, zaczynając od wszystkich jej wartości
wpadają we wskazane -sąsiedztwo punktu a.

Trzeba sobie wyobrazić proces zbliżania się do granicy dynamiki. wziąłem trochę - sąsiedztwo punktu a; zaczynając w pewnym momencie zmiany , wszystkie wartości mieszczą się w tej okolicy. Teraz przyjrzyjmy się bliżej - sąsiedztwo punktu a; zaczynając od pewnego (bardziej odległego w porównaniu z pierwszym) momentu zmiany , wszystkie jego wartości spadną - sąsiedztwo punktu ale itp. (rys. 1).

Po wprowadzeniu definicji granicy zmiennej staraliśmy się ją szczegółowo omówić i rozszyfrować. Jednak w tej definicji jeden bardzo istotny szczegół pozostał nieujawniony; co należy rozumieć przez słowa „począwszy od pewnego momentu zmiany zmiennej”? Widać to wyraźnie, gdy proces zmiany zmiennej przebiega w czasie: począwszy od pewnego momentu (czasu). Ale nie zawsze mamy do czynienia ze zmiennymi, które zmieniają się w czasie. Jak być w takich przypadkach? Wyjściem jest rozszyfrowanie tego miejsca w ogólnej definicji granicy zmiennej w określony sposób dla każdego typu zmiennych: na swój sposób dla sekwencji, na swój sposób dla funkcji i tak dalej.

Limit sekwencji. Przede wszystkim należy przypomnieć definicję ciągu: czy wszystkie wartości brane przez zmienną x, można ponumerować wszystkimi możliwymi liczbami naturalnymi x ), x 2 ,... x n,..., a wartość o wyższym numerze jest brana po wartości o mniejszej liczbie, to mówimy, że zmienna x przebiega przez sekwencję wartości x x, x 2 ,... x p...; lub po prostu, że istnieje sekwencja (sekwencja liczb).

Definicja. Sekwencja liczbowa wywoływana jest funkcja rzeczywista argumentu naturalnego, czyli funkcja, dla której = n I ER.

Jest oznaczony symbolem , gdzie , lub w skrócie . Liczba zależna od n nazywa się n – -ty element sekwencji. Układając wartości ciągu w kolejności numerycznej uzyskujemy, że ciąg można utożsamiać z przeliczalnym zbiorem liczb rzeczywistych, tj.

Przykłady:

a) Ciąg jest stały i składa się z równych liczb (jednostek): ;

b) . Dla niej

G) .

W przypadku ciągów stwierdzenie zawarte w ogólnej definicji granicy zmiennej „zaczyna się w pewnym momencie zmiany” " powinno oznaczać - "zaczynając od jakiejś liczby", ponieważ wyrazy o wyższych numerach następują (z definicji ciągu) za członem o niższej liczbie. Otrzymujemy więc następującą definicję granicy ciągu:

Definicja. Numer ale nazywa się limit ciągi jeśli dla dowolnej liczby istnieje taka liczba, że ​​wszystkie liczby dla których spełniają nierówność .

Odpowiednie oznaczenie

Nierówność można również zapisać jako lub . Te zapisy podkreślają, że wartość x n staje się arbitralnie niewiele różni się od a , gdy liczba członków wzrasta w nieskończoność. Geometrycznie definicja granicy ciągu oznacza: for dowolnie małe -sąsiedztwo liczby ale istnieje liczba N taka, że ​​wszystkie elementy ciągu większe niż N, liczby wpadają w to sąsiedztwo, poza sąsiedztwem znajduje się tylko skończona liczba członów początkowych ciągu (rys. 2). To są wszyscy lub niektórzy członkowie .

x 1 x 2 x N +1 a x N +2 x N x 3

Liczba w naszej definicji zależy od : n= N(). Jak wspomniano wcześniej, definicję granicy należy rozumieć w rozwoju, w dynamice, w ruchu: jeśli weźmiemy inną, mniejszą wartość dla , na przykład jest ogólnie mówiąc inny numer Nx > N, tak, że nierówności , jest zadowolony dla wszystkich .

Za pomocą symboli logicznych (kwantyfikatorów) napiszemy definicję granicy. Definicja granicy ciągu za pomocą kwantyfikatorów wygląda tak.

Powiązana zawartość:

1. Windows Virtual Machine Utwórz wirtualny system operacyjny
2. Jak utworzyć folder lub plik
3. Lekcja wideo: Jak utworzyć folder, jak utworzyć folder w folderze Jak otworzyć własny folder
4. Jak wybrać płyty główne do różnych zadań