VARIABILE ȘI CONSTANTE
Ca urmare a măsurătorii mărimi fizice(timp, suprafață, volum, masă, viteză etc.) se determină valorile numerice ale acestora. Matematica se ocupă de cantități, făcând abstracție din conținutul lor concret. În cele ce urmează, când vorbim de mărimi, ne vom referi la valorile lor numerice. În diferite fenomene, unele cantități se modifică, în timp ce altele își păstrează valoarea numerică. De exemplu, când un punct se mișcă uniform, timpul și distanța se schimbă, dar viteza rămâne constantă.
variabil Se numește o cantitate care ia diverse valori numerice. Se numește o cantitate ale cărei valori numerice nu se modifică permanent. Cantitățile variabile vor fi notate cu litere x, y, z,..., constant - a, b, c,...
Rețineți că la matematică constant adesea privit ca caz special variabilă în care toate valorile numerice sunt aceleași.
Schimbați zona O variabilă este totalitatea tuturor valorilor numerice pe care le acceptă. Zona de schimbare poate consta din unul sau mai multe intervale, sau dintr-un singur punct.
VARIABILĂ COMANDATĂ. SECVENȚA NUMERICALĂ
Vom spune că variabila X există variabilă ordonată, dacă aria modificării sale este cunoscută și pentru fiecare dintre oricare dintre valorile sale se poate spune care dintre ele este anterioară și care este următoarea.
Un caz special al unei variabile ordonate este o variabilă ale cărei valori se formează succesiune de numere x 1 ,x 2 ,…,x n ,… Pentru astfel de valori la i< j, i, j Î N , sens x i considerat a fi anterior, x j– ulterior, indiferent care dintre aceste valori este mai mare. Astfel, o secvență numerică este o variabilă ale cărei valori succesive pot fi renumerotate. Secvența numerică va fi notată cu . Numerele individuale ale unei secvențe se numesc ei elemente.
De exemplu, succesiunea numerică este formată din următoarele mărimi:
FUNCŢIE
Când se studiază diverse fenomene naturale și se rezolvă probleme tehnice și, în consecință, în matematică, trebuie să se ia în considerare modificarea unei cantități în funcție de modificarea alteia. Deci, de exemplu, se știe că aria unui cerc este exprimată în termeni de rază prin formula S = pr2. Dacă raza r ia diferite valori numerice, apoi aria S ia de asemenea diverse valori numerice, i.e. o modificare a unei variabile atrage după sine o modificare a celeilalte.
Dacă fiecare valoare a variabilei X, aparținând unei zone, corespunde unei valori specifice a altei variabile y, apoi y numit funcția variabilei x. Vom scrie simbolic y=f(x). În același timp, variabila X numit variabila independenta sau argument.
Înregistrare y=C, Unde C- constantă, denotă o funcție a cărei valoare, pentru orice valoare X la fel si egal C.
Multe valori X, pentru care este posibil să se determine valorile funcției y conform regulii f(x), se numește domeniul de aplicare al funcției.
Rețineți că o secvență numerică este și o funcție al cărei domeniu de definiție coincide cu mulțimea numerelor naturale.
Principalele funcții elementare includ toate funcțiile studiate la cursul de matematică școlar:
functie elementara este o funcție care poate fi dată de funcții și constante elementare de bază folosind un număr finit de operații de adunare, scădere, înmulțire, împărțire și preluare a unei funcții dintr-o funcție.
CONCEPTUL DE LIMITE A SECVENȚEI NUMERICE
În viitorul curs de matematică, conceptul de limită va juca un rol fundamental, deoarece conceptele de bază ale analizei matematice sunt direct legate de acesta - derivată, integrală etc.
Să începem cu conceptul de limită a unei secvențe numerice.
Număr A numit limită secvente X = {x n) dacă pentru un număr pozitiv arbitrar prealocat arbitrar mic ε există un astfel de număr natural N, asta pentru toti n>N inegalitatea |x n - a|< ε.
Dacă numărul A există o limită de secvență X = {x n), apoi spun asta x n tinde să A, si scrie .
Pentru a formula această definiție în termeni geometrici, introducem următoarea noțiune.
Vecinătatea punctului x 0 se numește interval arbitrar ( a, b) conţinând acest punct în interiorul său. Adesea se ia în considerare vecinătatea unui punct x0, pentru care x0 este mijlocul, atunci x0 numit centru cartierul și cantitatea ( b–A)/2 – rază Cartier.
Deci, să aflăm ce înseamnă geometric conceptul de limită a unei secvențe numerice. Pentru a face acest lucru, scriem ultima inegalitate din definiție în formă
Această inegalitate înseamnă că toate elementele secvenței cu numere n>N trebuie să se afle în intervalul (a – ε; a + ε).
Prin urmare, un număr constant A este limita succesiunii numerice ( x n) dacă pentru orice cartier mic centrat într-un punct A raza ε (ε sunt vecinătăți ale punctului A) există un astfel de element al șirului cu număr N că toate elementele ulterioare cu numere n>N va fi în acest cartier.
Exemple.
Să facem câteva remarci.
Observație 1. Evident, dacă toate elementele unei secvențe numerice iau aceeași valoare constantă x n = c, atunci limita acestei secvențe va fi egală cu constanta însăși. Într-adevăr, pentru orice ε inegalitatea | xn-c| = |c - c| = 0 < ε.
Observația 2. Din definirea unei limite rezultă că o secvență nu poate avea două limite. Într-adevăr, să presupunem că x n → ași în același timp x n → b. Luați oricare și marcați vecinătățile punctelor Ași b raza ε (vezi Fig.). Apoi, prin definirea limitei, toate elementele succesiunii, începând de la unele, trebuie să fie situate atât în vecinătatea punctului. A, iar în vecinătatea punctului b, ceea ce este imposibil.
Observația 3. Nu trebuie să ne gândim că fiecare succesiune numerică are o limită. Să fie, de exemplu, variabila să ia valorile 
. Este ușor de observat că această secvență nu tinde spre nicio limită.
LIMITA DE FUNCȚIE
Lasă funcția y=f(x) definite într-o vecinătate a punctului A. Să presupunem că variabila independentă X se apropie la infinit A. Asta înseamnă că putem da X valori arbitrar apropiate de A dar nu egali A. Să o notăm astfel x → a. Pentru așa X găsiți valorile corespunzătoare ale funcției. Se poate întâmpla ca valorile f(x) de asemenea, se apropie la infinit de un număr b.Atunci spun că numărul b există o limită de funcție f(x) la x → a.
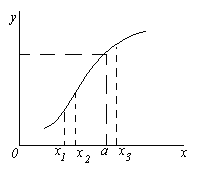
Să introducem o definiție riguroasă a limitei unei funcții.
Funcţie y=f(x) tinde spre limita b ca x → a, dacă pentru fiecare număr pozitiv ε, oricât de mic este acesta, se poate specifica un număr pozitiv δ astfel încât pentru toate x ≠ a din domeniul funcției care satisfac inegalitatea | x-a| < δ, имеет место неравенство |f(x) - b| < ε. Если b există o limită de funcție f(x) la x → a, apoi scrie sau f(x) → b la x → a.
Ilustram aceasta definitie pe graficul functiei. pentru că din inegalitate | x-a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при X Î ( A - δ, A+ δ) valorile corespunzătoare ale funcției f(x) Î ( b - ε, b+ ε), atunci, luând un arbitrar ε > 0, putem alege un număr δ astfel încât pentru toate punctele X, situat în δ, o vecinătate a punctului A, punctele corespunzătoare ale graficului funcției trebuie să se afle în interiorul unei benzi de lățime 2ε delimitată de drepte y=b– ε și y=b + ε.
Este ușor de observat că limita unei funcții trebuie să aibă aceleași proprietăți ca și limita unei secvențe numerice, și anume, dacă pt. x → a funcția are o limită, atunci este unică.
Exemple.
CONCEPTUL DE LIMITE DE FUNCȚIE LA UN PUNCT DE INTERNITATE
Până acum, am luat în considerare limite pentru cazul în care variabila X s-a străduit pentru un anumit număr constant.
Vom spune că variabila x tinde spre infinit, dacă pentru fiecare număr pozitiv predeterminat M(poate fi arbitrar mare) puteți specifica o astfel de valoare x=x 0, pornind de la care, toate valorile ulterioare ale variabilei vor satisface inegalitatea |x|>M.
De exemplu, lasă variabila X ia valori X 1 = –1, X 2 = 2, X 3 = –3, …, X n=(–1) n n,… Este clar că aceasta este o variabilă infinit de mare, deoarece pentru toți M> 0, toate valorile variabilei, începând de la unele, vor fi mai mari în valoare absolută M.
variabil x → +∞, dacă pentru un arbitrar M> 0, toate valorile ulterioare ale variabilei, începând de la o anumită, satisfac inegalitatea x > M.
De asemenea, X→ – ∞, dacă este cazul M > 0 X< -M .
Vom spune că funcția f(x) tinde spre limită b la X→ ∞ dacă pentru un număr pozitiv mic arbitrar ε se poate găsi un astfel de număr pozitiv M, care pentru toate valorile X satisfacerea inegalitatii |x|>M, inegalitatea | f(x) - b| < ε.
Desemna .
Exemple.
CARACTERISTICI INFINIT MARI
Mai devreme am luat în considerare cazurile în care funcția f(x) străduindu-se pentru o limită finală b la x → a sau X → ∞.
Luați în considerare acum cazul în care funcția y=f(x) o modalitate de a schimba argumentul.
Funcţie f(x) tinde spre infinit ca x → a, adică este infinit de mare valoare, dacă pentru orice număr M, oricât de mare ar fi, se poate găsi δ > 0 astfel încât pentru toate valorile X≠A, îndeplinind condiția | x-a| < δ, имеет место неравенство |f(x)| > M.
În cazul în care un f(x) tinde spre infinit ca x→a, apoi scrie sau f(x)→∞ la x→a.
Formulați o definiție similară pentru cazul când X→∞.
În cazul în care un f(x) tinde spre infinit ca x→ași în același timp ia numai valori pozitive sau numai negative, respectiv scrie sau .
Exemple.
FUNCȚII LIMITATE
Lasă funcția y=f(x), definit pe un anumit set D valorile argumentului.
Funcţie y=f(x) numit limitat pe platou D dacă există un număr pozitiv M astfel încât pentru toate valorile X din multimea luata in considerare, inegalitatea |f(x)|≤M. Dacă un astfel de număr M nu există, atunci funcția f(x) numit nelimitat pe platou D.
Exemple.
- Funcţie y=păcat X, definit la -∞<X<+∞, является ограниченной, так как при всех значениях X|păcat X|≤1 = M.
- Funcţie y=x 2 +2 este limitat, de exemplu, pe intervalul , deoarece pentru toți X din acest segment |f(x)| ≤f(3) = 11.
- Luați în considerare funcția y=ln X la Xн (0; 1). Această funcție este nemărginită pe segmentul indicat, deoarece pentru X→0 jurnal X→-∞.
Funcţie y=f(x) numit mărginită ca x → a dacă există un cartier centrat într-un punct A unde funcția este limitată.
Funcţie y=f(x) numit mărginită ca x→∞ dacă există un astfel de număr N> 0, care pentru toate valorile X |x|>N, funcție f(x) limitat.
Să stabilim o legătură între o funcție mărginită și o funcție care are o limită.
Teorema 1. Dacă și b este un număr finit, apoi funcția f(x) limitat la x→a.
Dovada. pentru că , atunci pentru orice ε>0 există un număr δ>0 astfel încât pentru toate valorile X satisfacerea inegalitatii |x-a|<
δ, inegalitatea |f(x) –b|<
ε. Folosind proprietatea modulului |f(x) – b|≥|f(x)| - |b|, scriem ultima inegalitate sub forma |f(x)|<|b|+
ε. Astfel, dacă punem M=|b|+ε, atunci x→a |f(x)|
Cometariu. Din definiția unei funcții mărginite rezultă că dacă , atunci este nemărginită. Cu toate acestea, inversul nu este adevărat: o funcție nemărginită poate să nu fie infinit de mare. Dă un exemplu.
Teorema 2. Dacă , atunci funcția y=1/f(x) limitat la x→a.
Dovada. Din condițiile teoremei rezultă că, pentru ε>0 arbitrar, într-o vecinătate a punctului A avem |f(x) – b|<
ε. pentru că |f(x) – b|=|b – f(x)| ≥|b| - |f(x)|, apoi |b| - |f(x)|<
ε. Prin urmare, |f(x)|>|b| -ε >0. De aceea 
2 Limită variabilă. Infinit de mic și infinit cantitati mari, relația dintre ei.
Limita unei variabile într-un anumit punct este numeric egală cu acest punct. limx(xàa) = a
Funcția se numește infinitezimală în punctul în care xàa dacă yà0. limf(x)_(xàa) = 0
Funcția se numește infinit mare în punctul în care xàa dacă yà0. limf(x)_(xàa) =<><>
Relația dintre cantități:
Dacă y=Ф(х) este infinit mic, atunci 1/Ф(х) este infinit bolnav
3 Infinit de mici, principalele lor proprietăți.
Suma unui număr finit de mărimi infinitezimale este o mărime infinitezimală.
Produsul unei funcții finite și al unei mărimi infinitezimale este o mărime infinitezimală.
Funcția din punctul a are o limită finită dacă și numai dacă f(x) = A + U(x), unde U(x) este o valoare infinitezimală.O altă modalitate de a scrie aceasta este f(x) – A à 0
Comparația funcțiilor infinitezimale:
Dacă limita raportului de un b.m. la alt b.m. este egal cu zero, apoi acel b.m., care era la numărător mai alb decât de ordin înalt. Dacă această limită este egală cu infinitul, atunci invers.
Și dacă limita raportului lor este egală cu un anumit număr, atunci aceste b.m. de aceeasi ordine.
Dacă limita este 1, atunci aceste două b.m. sunt echivalente.
Teorema 1: produsul infinitezimalelor este un infinitezimal de ordin mai mare decât oricare dintre ele.
AOD . Funcția a (x) se numește b / m dacă limita sa în acest t-ke este 0 din această definiție urmează următoarea proprietate a funcțiilor b / m:
a) Suma algebrică și produsul funcțiilor b/m sunt funcții b/m.
b) Produsul dintre o funcție b/m și o funcție mărginită este o funcție b/m, i.e. dacă a(x)®0 ca x®x0 și f(x) este definit și mărginit
Pentru a distinge b/m după viteza lor de tendință spre 0, se introduc următoarele. concept:
1) Dacă raportul de 2 b/m a(x)/b(x)®0 la x®x0 atunci ei spun că b/m a are un ordin mai mare de micime decât b.
2) Dacă a (x) / b (x) ® A¹0 cu x ® x0 (număr A), atunci a (x) și b (x) se numesc b / m de același ordin.
3) dacă a(x)/b(x)®1, atunci se spune că a(x) și b(x) sunt echivalente cu b/m (a(x)~b(x)), pentru x®x0 .
4) Dacă a (x) / b ^ n (x) ® A¹0, atunci a (x) se numește b / m de ordinul al n-lea față de b (x).
Definiții similare pentru cazurile: x®x0-, x®x0+, x®-¥, x®+¥ și x®¥.
4 Limita functiei. Teoreme de bază despre limite.
Definiție limită: fie φ(x) o funcție definită pe o mulțime X și a un punct limită al acestei mulțimi. Se numește numărul A limită funcții pentru x à a dacă și numai dacă pentru orice e există o vecinătate a punctului a astfel încât |f(x) – a|< |е|
Într-un alt mod, aceasta este scrisă ca f(x) à A pentru x à a
Teorema 1: Dacă fiecare termen al unei sume algebrice a unui număr finit de funcții are o limită pe măsură ce x tinde spre a, atunci limita acestei sume algebrice ca x este la a există și este egală cu aceeași sumă algebrică a limitelor termenilor.
Dovada: reprezentăm funcția ca sumă a limitei sale și infinitezimal, adunăm funcțiile și infinitezimal. Rezultă că suma funcțiilor diferă de suma limitelor printr-o infinitezimală, ceea ce înseamnă că aceasta este limita.
Consecinţă: O funcție poate avea o singură limită la x tulpini. la a. Dovedită prin contradicție. Se dovedește că diferența funcțiilor originale tinde spre diferența limitelor lor, adică zero tinde spre diferența limitelor și, deoarece limita unei funcții constante este egală cu funcția în sine și este unică, atunci de aici obținem că diferența de limită este 0, adică limitele sunt aceleași.
Teorema 2: Dacă fiecare dintre factorii produsului unui număr finit de funcții are o limită la x à a, atunci limita produsului la x rezultă la a este egală cu produsul limitelor factorilor.
dovada: Considerăm produsul a doi factori
Acasă > DocumentLIMITĂ. CONTINUITATEA FUNCȚIEI
VARIABILE ȘI CONSTANTE Ca urmare a măsurării mărimilor fizice (timp, suprafață, volum, masă, viteză etc.), se determină valorile numerice ale acestora. Matematica se ocupă de cantități, făcând abstracție din conținutul lor concret. În cele ce urmează, când vorbim de mărimi, ne vom referi la valorile lor numerice. În diferite fenomene, unele cantități se modifică, în timp ce altele își păstrează valoarea numerică. De exemplu, când un punct se mișcă uniform, timpul și distanța se schimbă, dar viteza rămâne constantă. variabil Se numește o cantitate care ia diverse valori numerice. Se numește o cantitate ale cărei valori numerice nu se modifică permanent. Cantitățile variabile vor fi notate cu litere x, y, z,..., constant - a, b, c,... Rețineți că în matematică o valoare constantă este adesea considerată ca un caz special al unei variabile în care toate valorile numerice sunt aceleași. Schimbați zona O variabilă este totalitatea tuturor valorilor numerice pe care le acceptă. Zona de schimbare poate consta din unul sau mai multe intervale, sau dintr-un singur punct. VARIABILĂ COMANDATĂ. SECVENȚA NUMERICALĂ Vom spune că variabila X există variabilă ordonată, dacă aria modificării sale este cunoscută și pentru fiecare dintre oricare dintre valorile sale se poate spune care dintre ele este anterioară și care este următoarea. Un caz special al unei variabile ordonate este o variabilă ale cărei valori se formează succesiune de numere X 1 ,X 2 ,…,X n ,… Pentru astfel de valori la i< j, i, j Î N , sens X i considerat a fi anterior, X j– ulterior, indiferent care dintre aceste valori este mai mare. Astfel, o secvență numerică este o variabilă ale cărei valori succesive pot fi renumerotate. Secvența numerică va fi notată cu . Numerele individuale ale unei secvențe se numesc ei elemente. De exemplu, succesiunea numerică este formată din următoarele mărimi:
FUNCŢIE Când se studiază diverse fenomene naturale și se rezolvă probleme tehnice și, în consecință, în matematică, trebuie să se ia în considerare modificarea unei cantități în funcție de modificarea alteia. Deci, de exemplu, se știe că aria unui cerc este exprimată în termeni de rază prin formula S = pr 2
. Dacă raza r ia diferite valori numerice, apoi aria S ia de asemenea diverse valori numerice, i.e. o modificare a unei variabile atrage după sine o modificare a celeilalte. Dacă fiecare valoare a variabilei X, aparținând unei zone, corespunde unei valori specifice a altei variabile y, apoi y numit funcția variabilei x. Vom scrie simbolic y=f(x). În același timp, variabila X numit variabila independenta sau argument. Înregistrare y=C, Unde C- constantă, denotă o funcție a cărei valoare, pentru orice valoare X la fel si egal C. Multe valori X, pentru care este posibil să se determine valorile funcției y conform regulii f(x), se numește domeniul de aplicare al funcției. Rețineți că o secvență numerică este și o funcție al cărei domeniu de definiție coincide cu mulțimea numerelor naturale. Principalele funcții elementare includ toate funcțiile studiate la cursul de matematică școlar: functie elementara este o funcție care poate fi dată de funcții și constante elementare de bază folosind un număr finit de operații de adunare, scădere, înmulțire, împărțire și preluare a unei funcții dintr-o funcție. CONCEPTUL DE LIMITE A SECVENȚEI NUMERICEÎn viitorul curs de matematică, conceptul de limită va juca un rol fundamental, deoarece conceptele de bază ale analizei matematice sunt direct legate de acesta - derivată, integrală etc. Să începem cu conceptul de limită a unei secvențe numerice. Număr A numit limită secvente X = {X n) dacă pentru un număr pozitiv arbitrar prealocat arbitrar mic ε există un astfel de număr natural N, asta pentru toti n>N inegalitatea |x n - a|< ε. Если число A există o limită de secvență X = {X n), apoi spun asta X n tinde să A, si scrie . Pentru a formula această definiție în termeni geometrici, introducem următoarea noțiune. Vecinătatea punctului x 0
se numește interval arbitrar ( a, b) conţinând acest punct în interiorul său. Adesea se ia în considerare vecinătatea unui punct X 0
, pentru care X 0
este mijlocul, atunci X 0
numit centru cartierul și cantitatea ( b–A)/2 – rază Cartier. Deci, să aflăm ce înseamnă geometric conceptul de limită a unei secvențe numerice. Pentru a face acest lucru, scriem ultima inegalitate din definiție în formă Această inegalitate înseamnă că toate elementele secvenței cu numere n>N trebuie să se afle în intervalul (a – ε; a + ε). DIN 
prin urmare, un număr constant A este limita succesiunii numerice ( X n) dacă pentru orice cartier mic centrat într-un punct A raza ε (ε sunt vecinătăți ale punctului A) există un astfel de element al șirului cu număr N că toate elementele ulterioare cu numere n>N va fi în acest cartier. Exemple.
- Lasă variabila X ia valori succesiv
, apoi pentru a îndeplini relația |x n - a|< ε достаточно, чтобы или . Поэтому, взяв в качестве N orice număr natural care satisface inegalitatea, obținem ceea ce ne trebuie. Deci, dacă luăm, de exemplu, , atunci, setarea N= 6, pentru toată lumea n>6 vom avea 
. Luați un ε arbitrar > 0. Considerăm . Atunci , dacă sau , adică . Prin urmare, alegem orice număr natural care satisface inegalitatea . Să facem câteva remarci. Observație 1. Evident, dacă toate elementele unei secvențe numerice iau aceeași valoare constantă X n = c, atunci limita acestei secvențe va fi egală cu constanta însăși. Într-adevăr, pentru orice ε inegalitatea | X n -c| = |c - c| = 0 < ε. W 
nota 2. Din definirea unei limite rezultă că o secvență nu poate avea două limite. Într-adevăr, să presupunem că X n → ași în același timp X n →b. Luați oricare și marcați vecinătățile punctelor Ași b raza ε (vezi Fig.). Apoi, prin definirea limitei, toate elementele secvenței, începând de la unele, trebuie să fie situate atât în vecinătatea punctului. A, iar în vecinătatea punctului b, ceea ce este imposibil. Observația 3. Nu trebuie să ne gândim că fiecare succesiune numerică are o limită. Să fie, de exemplu, variabila să ia valorile 
. Este ușor de observat că această secvență nu tinde spre nicio limită. | LIMITA DE FUNCȚIE Lasă funcția y=f(x) definite într-o vecinătate a punctului A. Să presupunem că variabila independentă X se apropie la infinit A. Asta înseamnă că putem da X valori arbitrar apropiate de A dar nu egali A. Să o notăm astfel x → a. Pentru așa X găsiți valorile corespunzătoare ale funcției. Se poate întâmpla ca valorile f(x) de asemenea, se apropie la infinit de un număr b.Atunci spun că numărul b există o limită de funcție f(x) la x → a. Să introducem o definiție riguroasă a limitei unei funcții. Funcţie y=f(x) tinde spre limita b ca x → a, dacă pentru fiecare număr pozitiv ε, oricât de mic este acesta, se poate specifica un număr pozitiv δ astfel încât pentru tot x ≠ a din domeniul funcției | x-a| < δ, имеет место неравенство |f(x) - b| < ε. Если b există o limită de funcție f(x) la x → a, apoi scrie sau f(x) → b la x → a. Ilustram aceasta definitie pe graficul functiei. pentru că din inegalitate | x-a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при X Î ( A - δ, A+ δ) valorile corespunzătoare ale funcției f(x) Î ( b - ε, b+ ε), atunci, luând un arbitrar ε > 0, putem alege un număr δ astfel încât pentru toate punctele X, situat în δ, o vecinătate a punctului A, punctele corespunzătoare ale graficului funcției trebuie să se afle în interiorul unei benzi de lățime 2ε delimitată de drepte y=b– ε și y=b+ e. Este ușor de observat că limita unei funcții trebuie să aibă aceleași proprietăți ca și limita unei secvențe numerice, și anume, dacă pt. x → a funcția are o limită, atunci este unică. Exemple. Folosind graficul unei funcții date, este ușor de observat că . |
|
CONCEPTUL DE LIMITE DE FUNCȚIE ÎNTR-UN PUNCT INFINIT DEPISTAT Până acum, am luat în considerare limite pentru cazul în care variabila X s-a străduit pentru un anumit număr constant. Vom spune că variabila x tinde spre infinit, dacă pentru fiecare număr pozitiv predeterminat M(poate fi arbitrar mare) puteți specifica o astfel de valoare x=x 0
, pornind de la care, toate valorile ulterioare ale variabilei vor satisface inegalitatea |x|>M. De exemplu, lasă variabila X ia valori X 1 = –1, X 2 =
2, X 3 = –3, …, X n=(–1) n n,… Este clar că aceasta este o variabilă infinit de mare, deoarece pentru toți M> 0, toate valorile variabilei, începând de la unele, vor fi mai mari în valoare absolută M. variabil x → +∞, dacă pentru un arbitrar M> 0, toate valorile ulterioare ale variabilei, începând de la o anumită, satisfac inegalitatea x > M. De asemenea, X→ – ∞, dacă este cazul M > 0 X< -M
. Vom spune că funcția f(x) tinde spre limită b la X→ ∞ dacă pentru un număr pozitiv mic arbitrar ε se poate găsi un astfel de număr pozitiv M, care pentru toate valorile X satisfacerea inegalitatii |x|>M, inegalitatea | f(x) - b| < ε. Обозначают . Exemple. H 
Este necesar să se demonstreze că pentru un ε arbitrar inegalitatea se va menține de îndată ce |x|>M, și numărul M trebuie determinată de alegerea lui ε. Inegalitatea scrisă este echivalentă cu următoarea, ceea ce va fi valabil dacă |x|> 1/ε=M. Aceasta înseamnă că (vezi fig.). CARACTERISTICI INFINIT MARI Mai devreme am luat în considerare cazurile în care funcția f(x) străduindu-se pentru o limită finală b la x → a sau X→∞. Luați în considerare acum cazul în care funcția y=f(x) o modalitate de a schimba argumentul. Funcţie f(x) tinde spre infinit ca x → a, adică este infinit de mare valoare, dacă pentru orice număr M, oricât de mare ar fi, se poate găsi δ > 0 astfel încât pentru toate valorile X≠A, îndeplinind condiția | x-a| < δ, имеет место неравенство |f(x)| > M. În cazul în care un f(x) tinde spre infinit ca x→a, apoi scrie sau f(x)→∞ la x→a. Formulați o definiție similară pentru cazul când X→∞. În cazul în care un f(x) tinde spre infinit ca x→aşi în acelaşi timp ia numai valori pozitive sau numai negative, respectiv scrie sau . Exemple. 
FUNCȚII LIMITATE Lasă funcția y=f(x), definit pe un anumit set D valorile argumentului. Funcţie y=f(x) numit limitat pe platou D dacă există un număr pozitiv M astfel încât pentru toate valorile X din multimea luata in considerare, inegalitatea |f(x)|≤M. Dacă un astfel de număr M nu există, atunci funcția f(x) numit nelimitat pe platou D. Exemple.
- Funcţie y=păcat X, definit la -∞<X<+∞, является ограниченной, так как при всех значениях X|păcat X|≤1 = M. Funcţie y=x 2 +2 este limitat, de exemplu, pe intervalul , deoarece pentru toți X din acest segment |f(x)| ≤f(3) = 11. Se consideră funcția y=ln X la Xн (0; 1). Această funcție este nemărginită pe segmentul indicat, deoarece pentru X→0 jurnal X→-∞.
. FUNCȚII INFINIT MARI ȘI INFINIT MICI
FUNCȚIILE INFINIT DE MICI ȘI PRINCIPALELE LOR PROPRIETĂȚI Funcţie y=f(x) numit infinitezimal la x→a sau când X→∞ dacă sau , adică O funcție infinitezimală este o funcție a cărei limită într-un punct dat este zero. P
exemple. 
Să stabilim următoarea relație importantă: Teorema. Dacă funcţia y=f(x) reprezentabil la x→a ca sumă a unui număr constant bși infinit de mici α(x): f(x)=b+ α(x) apoi . În schimb, dacă , atunci f(x)=b+α(x), Unde topor) este infinit de mic la x→a. Dovada. Să luăm în considerare principalele proprietăți ale funcțiilor infinitezimale. Teorema 1. Suma algebrică a doi, trei și, în general, orice număr finit de infinitezimale este o funcție infinitezimală. Dovada. Să dăm o dovadă pentru doi termeni. Lăsa f(x)=α(x)+β(x), unde și . Trebuie să demonstrăm că pentru ε arbitrar arbitrar mic >
0 acolo δ>
0, astfel încât pt X satisfacerea inegalitatii |x – a|<δ
, efectuat |f(x)|<
ε. Astfel, fixăm un număr arbitrar ε >
0. Deoarece, conform ipotezei teoremei, α(x) este o funcție infinitezimală, atunci există δ 1 >
0, care la |x – a|<
δ 1 avem |α(x)|<
ε /
2.
La fel, din moment ce β(x) este infinitezimal, atunci există un astfel de δ 2 >
0, care la |x – a|<
δ 2 avem | β(x)|<
ε /
2.
Hai sa luam δ=min(δ1 ,
δ2 }
.Apoi într-o vecinătate a punctului A rază δ
fiecare dintre inegalităţi va fi satisfăcută |α(x)|<
ε /
2 și | β(x)|<
ε /
2.
Prin urmare, în acest cartier va exista |f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|<
ε /2 +
ε /2=
ε, adică |f(x)|<
ε, care trebuia demonstrat. Teorema 2. Produsul unei funcții infinitezimale topor) pentru o funcție limitată f(x) la x→a(sau când x→∞) este o funcție infinitezimală. Dovada. Din moment ce functia f(x) este limitat, atunci există un număr M astfel încât pentru toate valorile X dintr-o vecinătate a punctului a|f(x)|≤M.În plus, din moment ce topor) este o funcție infinitezimală pentru x→a, apoi pentru ε arbitrar >
0 există o vecinătate a punctului A, în care inegalitatea |α(x)|<
ε /M. Apoi, în cel mai mic dintre aceste cartiere avem | αf|<
ε /M= ε. Și asta înseamnă că af- infinit de mici. Pentru cazul x→∞ dovada se realizează în mod similar. Din teorema demonstrată rezultă: Consecința 1. Dacă și , atunci . Consecința 2. Dacă și c= const, atunci . Teorema 3. Raportul unei funcții infinitezimale α(x) per functie f(x), a cărei limită este diferită de zero, este o funcție infinitezimală. Dovada. Lăsa 
. Apoi 1 /f(x) există o funcție limitată. Prin urmare, fracția 
este produsul unei funcții infinitezimale și al unei funcții mărginite, i.e. funcția este infinitezimală. 1. Semnificația generală culturală și practică a paradigmei continuității și calculului diferențial și integral
abstractAnexa 1 Elemente de aplicare a matematicii în cercetarea socio-economică și socio-managerială și în practica modernă a afacerilor - posibile teme aplicate pentru rezumate,
- Document
Acest capitol descrie nume valide de variabile și funcții Mathcad, variabile predefinite precum acestea și reprezentări numerice Mathcad gestionează numerele complexe la fel de ușor ca și numerele reale.
„Funcții și grafice”
abstractAș dori să aflu mai multe despre ce este o funcție și graficele funcției. Din clasa a VII-a studiem algebra conform programului lui A.G. Mordkovici. Consider că conceptul de dependență funcțională este unul dintre conceptele centrale în matematică și pătrunde în toate aplicațiile sale.
Scurtă prezentare generală și manual de referință. Cartea este prima revizuire și manual de referință de acest fel despre fizica virtuală și este destinată unei game largi de cititori interesați de problemele științei în general și ale fizicii în special.
CarteCartea este prima revizuire și manual de referință de acest fel despre fizica virtuală și este destinată unei game largi de cititori interesați de problemele științei în general și ale fizicii în special.
Programul examenelor de admitere la magistratură în direcţia 010200. 68 Matematică. Matematică aplicată „Analiza matematică”
ProgramLimita succesiunii numerice. Proprietăți principale: unicitatea limitei; limitele secvenței convergente; convergența unei subsecvențe a unei secvențe convergente.
Dintre diferitele moduri de comportament ale variabilelor, cel mai important este cel în care variabila tinde către o anumită limită. În acest caz, valorile luate de variabilă X, devin în mod arbitrar aproape de un număr constant A- limita acestei variabile. Se spune că o variabilă tinde să se apropie la infinit de un număr constant A(la limita ta). Să oferim mai detaliat definiția corespunzătoare.
Variabila x tinde spre limita a (a - număr constant) dacă valoarea absolută diferența dintre x și a devine arbitrar mică în procesul de modificare a variabilei.
Aceeași definiție poate fi spusă și cu alte cuvinte.
Definiție.Numărul constant a este numitlimită variabilăx dacă - valoarea absolută a diferenței dintre x și a devine arbitrar mică în procesul de modificare a variabilei x.
Faptul că numărul A, este limita unei variabile, se scrie astfel:
( - primele litere ale cuvântului limes - limită) sau X-> a
Să clarificăm ce ar trebui înțeles prin cuvintele „valoarea devine arbitrar mică”, care sunt disponibile în definiția limitei. Să luăm un număr pozitiv arbitrar , atunci, dacă, începând de la un anumit moment al schimbării variabilei X, valorile vor deveni și vor deveni mai mici decât aceasta 
.
Variabila tinde spre limită dacă pentru orice pozitiv . începând de la un moment dat în schimbarea variabilei , inegalitatea este îndeplinită 
.
Definiția unei limite are o semnificație geometrică simplă: inegalitatea înseamnă că se află în vecinătatea punctului , i.e. în interval (Fig. 26). Deci definiția limitei în formă geometrică este: un număr este limita unei variabile dacă pentru oricare (arbitrar mic)-vecinatatea unui punct puteți specifica un astfel de moment în schimbarea unei variabile, începând de la care toate valorile acesteia
se încadrează în -vecinatatea indicată a punctului a.
Este necesar să ne imaginăm procesul de apropiere a limitei în dinamică. a luat câteva - vecinătatea punctului A; începând la un moment dat în schimbare , toate valorile se încadrează în acest cartier. Acum să ne apropiem - vecinătatea punctului A; plecând de la un moment (mai îndepărtat în comparaţie cu primul) al schimbării , toate valorile sale vor cădea în - vecinătatea punctului A etc. (Fig. 1).
 |
|||
 |
|||
După ce am introdus definiția limitei unei variabile, am încercat să o discutăm și să o descifrăm în detaliu. Cu toate acestea, în această definiție, un detaliu foarte semnificativ a rămas nedezvăluit; ce ar trebui să se înțeleagă prin cuvintele „începând dintr-un anumit moment în schimbarea variabilei”? Acest lucru este clar atunci când procesul de modificare a variabilei decurge în timp: începând de la un anumit moment (timp). Dar nu avem întotdeauna de-a face cu variabile care se schimbă în timp. Cum să fii în aceste cazuri? Ieșirea este de a descifra acest loc în definiția generală a limitei unei variabile într-un mod specific pentru fiecare tip de variabile: în felul său pentru secvențe, în felul său pentru funcții și așa mai departe.
Limită de secvență.În primul rând, este necesar să ne amintim definiția unei secvențe: dacă toate valorile sunt luate de o variabilă X, poate fi numerotat folosind toate numerele naturale posibile x ), x 2 ,... x n,..., iar valoarea cu un număr mai mare se ia după valoarea cu un număr mai mic, atunci spunem că variabila X parcurge o succesiune de valori x x, x 2 ,... x p...; sau pur și simplu că există o secvență (secvență numerică).
Definiție. Succesiunea numerică se numește o funcție reală a unui argument natural, adică o funcție pentru care = N și ER.
Este notat cu simbolul , unde , sau pe scurt, . Un număr care depinde de n se numește n – al-lea membru al secvenței. Aranjand valorile secvenței în ordine numerică, obținem că șirul poate fi identificat cu un set numărabil de numere reale, adică.
Exemple:
a) Sirul este constant si este format din numere (unitati) egale: ;
b) 
. Pentru ea
G) 
.
Pentru secvențe, enunțul conținut în definiția generală a limitei unei variabile „începând la un moment dat în schimbare " ar trebui să însemne - „începând de la un număr”, întrucât termenii cu numere mai mari urmează (prin definiția succesiunii) membrului cu un număr mai mic. Deci obținem următoarea definiție a limitei unei secvențe:
Definiție. Număr A numit limită secvențe dacă pentru orice număr există un număr astfel încât toate numerele pentru care satisfac inegalitatea .
Denumirea adecvată
Inegalitatea poate fi scrisă și ca 
sau . Aceste înregistrări subliniază faptul că valoarea x n devine în mod arbitrar puțin diferit de A , când numărul membrului crește la nesfârșit. Din punct de vedere geometric, definirea limitei unei secvențe înseamnă următoarele: pentru arbitrar mic - vecinătatea numărului A există un număr N astfel încât toți membrii secvenței cu mai mare decât N, numerele cad în acest cartier,în afara vecinătății este doar un număr finit de termeni inițiali ai secvenței (Fig. 2). Aceștia sunt toți sau unii dintre membri .
x 1 x 2 x N +1 a x N +2 x N x 3
Numărul din definiția noastră depinde de : N= N(). După cum am menționat mai devreme, definiția limitei trebuie înțeleasă în dezvoltare, în dinamică, în mișcare: dacă luăm o altă valoare, mai mică, pentru , de exemplu, există, în general, un alt număr N x > N, astfel încât inegalitatea , este multumit pentru toti .
Vom scrie definiția limitei folosind simboluri logice (cuantificatori). Definirea limitei unei secvențe folosind cuantificatori arată astfel.
Fie x o variabilă ordonată (de exemplu, o secvență numerică).
Definiție.
număr constantAse numește limita variabilei x, dacă există un număr pozitiv arbitrar mic nu am luat, puteți specifica o astfel de valoare a variabilei x încât toate valorile ulterioare ale variabilei vor satisface inegalitatea X-A .
În mod simbolic, aceasta se scrie xa sau limx = a (din latinescul limes - limită).
Geometric această definiție înseamnă că oricât de mică - vecinătatea punctului a pe care o luăm, toate valorile ulterioare ale lui x după unele vor fi în această vecinătate.
Din figură se poate observa că inegalitatea 
înseamnă că distanța de la punctul x la a este mai mică decât . Și acesta este interiorul cartierului. Punctul x satisface evident dubla inegalitate a- 
si sunt echivalente.
O 
definiție: Pentru o succesiune numerică (x n ), a este limita dacă, conform 
puteți specifica un numărN astfel încât pentru toți 
Pentru membrii secvenței, toate valorile x N , x N +1 și mai departe se află în interior 
- Cartierul este o necesitate.
O variabilă x ale cărei valori formează o secvență numerică x 1 ,x 2 ,…,x n este adesea scrisă ca membru al șirului x=x n sau (x n ). De exemplu, (1/n). Aceasta este o variabilă sau o secvență cu un termen comun x n =1/n: 1.1/2.1/3...
Exemplu: Fie ca variabila x să ia valori succesive: x 1 =2/1, x 2 =3/2, x 3 =4/3, …,x n =(n+1)/n,… adică. formează o secvență de numere. Să demonstrăm asta 
.
Hai sa luam 
.
. De îndată ce numărul devine 
, o vom lua drept N. Atunci inegalitatea va ține pentru 
. Dar apoi totul este dovedit.
Teorema 1: limita unei constante este egală cu această constantă. Dovada: O valoare constantă este un caz special al unei variabile - toate valorile sale \u003d c: x \u003d c / Dar, atunci limc \u003d c.
Teorema 2: Variabila x nu poate avea două limite.
Dovada: Să spunem limx=a și limx=b. Apoi 
și 
după o anumită valoare a lui x. Dar apoi
pentru că 
arbitrar mic, atunci inegalitatea este posibilă numai pentru a=b
Notă: Este posibil ca variabila să nu aibă o limită: x=x n =(-1) n =-1,+1,-1,+1. Distanța până la orice punct a de la valorile sale –1,+1 nu poate fi mai mică de 1/2 
(-1) n nu are limită.
Am presupus că a este un număr. Dar variabila x poate tinde și spre infinit.
Definiție: Variabila x tinde spre infinit dacă pentru 
pornind de la o valoare x, valorile rămase satisfac inegalitatea 
. Variabila x tinde să 
, dacă în aceleași condiții inegalitatea x>M este satisfăcută și k - 
, dacă în aceleași condiții inegalitatea x<-M.
Если переменная X
стремится к бесконечности, то её называют
infinit de mare si scrie 
Exemplu: x=xn=n2. Hai sa luam 
>0. Trebuie efectuat n 2 >M. n> 
. De îndată ce n satisface această inegalitate, atunci pentru tot x n = n 2 inegalitatea este valabilă. Deci n 2 
, sau mai bine zis n 2 
.
§3. Limita functiei.
Vom presupune că argumentul x al funcției y=f(x) tinde spre x 0 sau .
Luați în considerare comportamentul funcției y în aceste cazuri.
Definiție.
Fie definită funcția y=f(x) într-o vecinătate a punctului x 0 . Numărul A se numește limita funcției la xx 0, dacă pentru orice , arbitrar mic, puteți specifica un astfel de număr încât pentru toate xx 0 și să satisfacă inegalitatea x-x 0 inegalitatea f (x)-A.
Dacă A este limita funcției f(x), atunci scriem 
sau f(x)A la xx 0.
O 
Definiția poate fi ilustrată în acest fel geometric.
Dacă A este limita lui f (x) la xx 0, atunci luând orice -vecinătate a punctului A, putem indica întotdeauna o astfel de - vecinătate a punctului x 0 încât pentru tot x din acest - vecinătatea valorii funcției f (x) sunt separate de A nu mai mult de , adică. se încadrează în vecinătatea aleasă a punctului A sau, oricum, partea din grafic corespunzătoare punctelor x din vecinătatea se află în întregime într-o fâșie de lățime 2.
Se poate observa că cu cât este mai mic, cu atât mai mic ar trebui să fie .
Definiție.
Fie argumentul x tinde spre punctul x 0, luând tot timpul valorile xx 0 xx 0 . Apoi numărul A 1 (A 2), către care tinde funcția f (x), se numește limita funcției f (x) în punctul x 0 din dreapta (stânga) sau dreptaci (stângaci).
Se scrie: lim x x0 + 0 f (x) \u003d A 1, (lim x x0-0 f (x) \u003d A 2).
Se poate dovedi că dacă limita lim x x0 f(x)=A există, atunci ambele limite unilaterale există în acest punct și sunt egale, A 1 =A 2 =A. Dimpotrivă: dacă există limite unilaterale și sunt egale, atunci există o limită comună. Dacă cel puțin unul nu există sau nu sunt egali, atunci limita funcției nu există.
Exemplu.
Demonstrați că f(x)=3x-2 are o limită la x1 egală cu 1.
Orice 3.
Ca puteți lua orice numere pozitive /3; 0</3.
Am demonstrat că pentru orice este suficient să luăm /3 astfel încât de la 0х f(х)-1, dar asta înseamnă că lim X (3x-2)=1.
Definiție.
H 
cuvântul A se numește limita funcției y=f(x) la x, dacă pentru orice (arbitrar mic) se poate specifica un număr pozitiv P astfel încât pentru toate valorile x care satisfac inegalitatea х P inegalitatea f(x)-A.
Scrieți lim x f(x)=A.
Geometric, aceasta înseamnă că pentru orice graficul funcției pentru xp și x-p este situat într-o fâșie cu lățimea de 2.
Exemplu.
f(x)=1/x la x, f(x)0.
Oricare ar fi 0, graficul funcției la xP și x-P va fi situat într-o bandă cu lățimea de 2.
1/х, 1/х, x1/, Р=1/.
În mod similar, sunt definite și 
f(x)=A 1 și 
f (x) \u003d A 2. În primul caz, inegalitatea f(x)-A 1 pentru xP trebuie satisfăcută, în al doilea caz f(x)-A 2 pentru x-P (P0 .
Asa de, 
1/x=0 și 
1/x=0. Egalitatea lor ne permite să luăm în considerare limita generală 
1/x=0.
